以前の熱化学方程式の記事には、
かなりの人が興味を持ってくれたようです。
しかし前回の記事は初心者向けだったので、
エネルギー図の練習は不十分だったと思います。
そこで今回の記事では、
エネルギー図の書き方を復習した上で、
エネルギー図習得に十分な演習問題を用意しました。
かなりボリュームのある記事ですが、
この記事を最後まで読むだけで、
熱化学方程式が得意科目になることでしょう。
ぜひ紙とペンを用意して、
一緒に解きながら勉強していきましょう。
目次
エネルギー図の書き方
たった２つの事実を理解していれば、
エネルギー図は簡単に書くことができます。
それは、
①エネルギーの高低を覚える
②エネルギー・熱の意味を理解する
です。
言葉だけ聞いてもわからないと思うので、
それぞれ順番に意味を確認します。
①エネルギーの高低を覚える
例えば酸素原子Oの状態よりも、
O2やH2Oの方が安定に存在します。
さらに化合物の中でも、
黒鉛CはCO2よりエネルギーが高いので、
燃えてCO2になりやすいですね。
このように、
物質のエネルギーの高低は決まっています。
エネルギーの高低は以下の順番になります。
まずはこれを覚える必要があるのですが、
具体例をイメージすればそんなに大変じゃないです。
例えば、
自然界には単体より化合物が多いですから、
単体 > 化合物と想像できそうですし、
物が燃えれば熱放出して燃焼物になるので、
化合物 > 完全燃焼物になります。
もちろん単体より原子状態は不安定だし、
電荷の偏りが出ればさらに不安定ですから、
イオン > 原子 > 単体です。
まあとにかく、
具体例をイメージするにしてもしないにしても、
まずはこのエネルギーの順番を覚えておきましょう。
酸化数が最大になるまで酸化された化合物と考えれば良いです。CO2は完全燃焼物として扱いますが、COは化合物として扱います。
②エネルギー・熱の意味を理解する
化学の世界では、
エネルギーとは「必要なエネルギー」を意味し、
熱は「放出するエネルギー」を意味します。
エネルギーは与える物、熱は捨てるものであり、
エネルギーを与えればエネルギーが高くなり、
熱を捨てればエネルギーが低くなります。
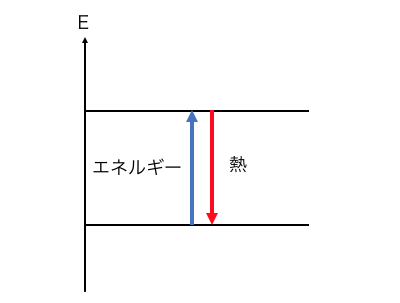
結合エネルギーによって単体→原子になり、
燃焼熱を放出して化合物→完全燃焼物になる、
と言うことからも想像できると思います。
エネルギー図を書く上でかなり重要なので、
よーく頭に残しておいてください。
つまり、
・燃焼熱
・生成熱
・溶解熱
など「熱」がつくものは下矢印、
・結合エネルギー
・格子エネルギー
・イオン化エネルギー
など「エネルギー」がつくものは上矢印で書きます。
これらを一つの図にまとめると以下の通り。
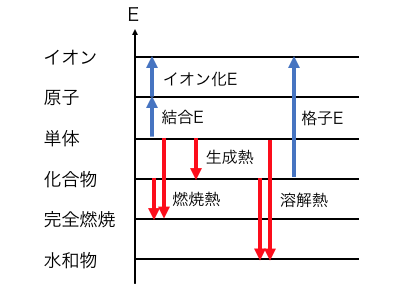
この図はわざわざ覚えなくても、
問題文を読めばその場で作れます。
まとめれば、
・エネルギーの順番
・エネルギーは上矢印、熱は下矢印
を覚えることでエネルギー図を書く準備は完了です。
一緒にエネルギー図を書いてみよう！
それでは実際の問題を使って、
一緒にエネルギー図を書いてみましょう。
この記事を目で眺めるだけでもいいですが、
できれば自分のノートに書いてみるといいです。
今回の例題は以下の通りです。
エタンの生成熱を求めよ。ただし固体炭素C、水素H2、エタンC2H6の燃焼熱はそれぞれ394kJ/mol、286kJ/mol、1560kJ/molとする。
①まずは求めたい熱の式を書き込む
エネルギー図に書き込んでいくのですが、
まずは先ほど覚えたエネルギーの順を書きます。
今回は単体、化合物、完全燃焼物だけなので、
以下のようなエネルギー図の型を用意します。
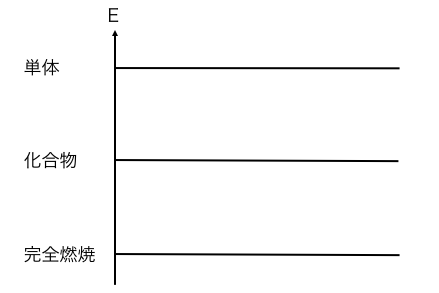
早速ここに求めたい熱を含む式を書きます。
求めたいのは生成熱なので、矢印は下向きです。
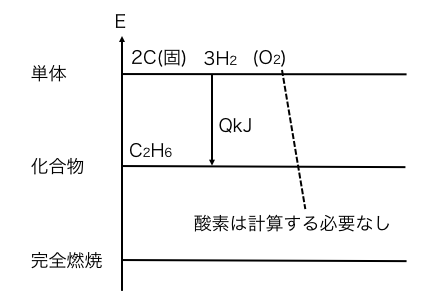
②次に残りの式を書き込む
それでは残りの式も書き込みましょう。
まずはH2の燃焼熱。
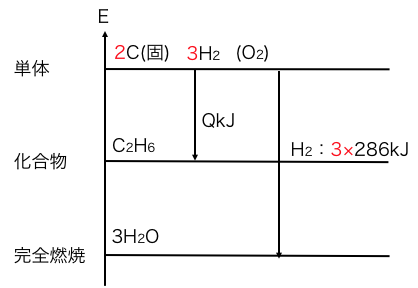
次にCの燃焼熱。
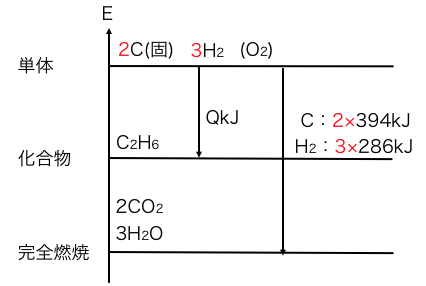
単体の段階から完全燃焼物に行くには、
2つのCと3つのH2を燃やすので、
それらの燃焼熱の合計が放出されます。
最後にエタンの燃焼熱。
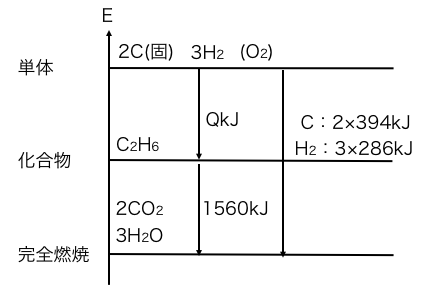
これによってエネルギー図完成です。
③図から方程式を立てて解く
ここまで来たら問題は解けたも同然！
エネルギー図を見て方程式を立て、
実際にQを求めましょう。
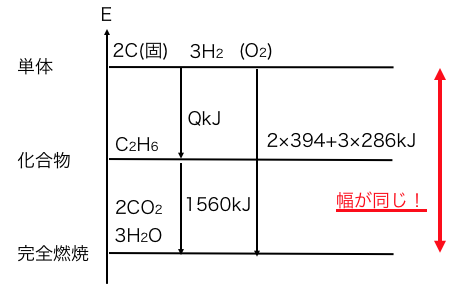
\begin{align*}
\mathrm{ Q + 1560 } &\mathrm{ = 2\times394 + 3\times286 } \\
\mathrm{ Q } &\mathrm{ = 86 }
\end{align*}
補足：エネルギー図はいつでも書ける？
エネルギー図は「ヘスの法則」を根拠にしています。
ある物質からある物質への反応熱は、
反応の経路によらない、と言う法則です。
だから基本的にはどんな問題もエネルギー図で解くことができます。
ただ少し「？？」となるパターンもあるので、
それは次の演習問題の中で確認しましょう。
演習問題
今回は基礎的なものから難し目なものまで、
少し多めに問題を用意しておきました。
ここの問題をきちんと解くことができれば、
エネルギー図はもう完璧でしょう。
ぜひ自分で解いてみてください。
①結合エネルギーと反応熱
（解答）
求めたい結合エネルギーをQとして、
原子、単体、化合物のエネルギー図に、
アンモニアの解離反応を書き込みます。
アンモニアにはN-Hが3つあることに注意です。
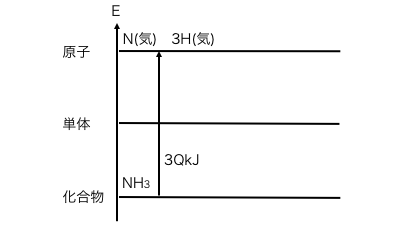
次に水素、窒素の解離を、
両方一気に書いてしまいます。
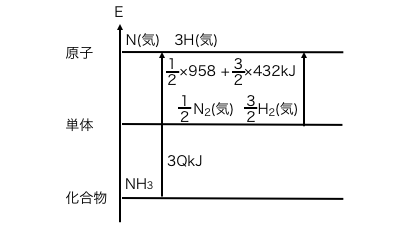
最後にアンモニアの生成熱を書きます。
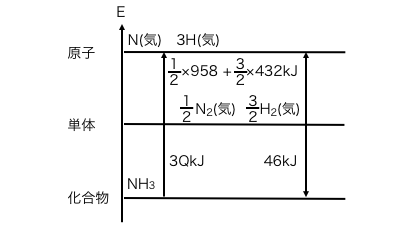
以上を計算すれば、
\(\mathrm{ 3Q = (\frac{1}{2}\times958+\frac{3}{2}\times432)+46 }\)
\(\mathrm{ Q = 391kJ}\)
②結合エネルギーと反応熱
\(\mathrm{ 2C(固) + 3H_{2} = C_{2}H_{6} + 84kJ }\)
\(\mathrm{ C(固) = C(気) – 715kJ }\)
またC=Cの結合エネルギーが590kJの時、以下の反応熱Qも求めよ。
\(\mathrm{ C_{2}H_{4} + H_{2} = C_{2}H_{6} + QkJ }\)
（解答）
求めたい結合エネルギーをqとして、
原子、単体、化合物のエネルギー図に、
エタンの解離反応を書き込みます。
C-Cは1つ、C-Hは6つあることに注意です。
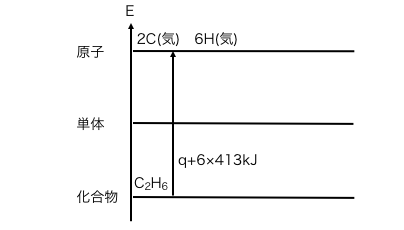
次に水素炭素のの解離を一気に書きます。
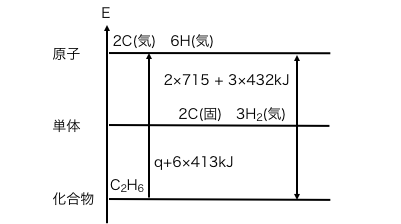
最後にエタンの生成熱を書きます。
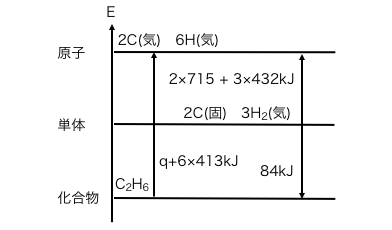
以上を計算すれば、
\(\mathrm{ q + 6\times413 = (2\times715+3\times432)+84 }\)
\(\mathrm{ q = 332kJ}\)
次にQを求めるのですが、
ここではヘスの法則を体感するために、
少しだけ違う考え方も紹介します。
以下のように左辺と右辺のエネルギーを考え、
その差分がQになる、と考えます。
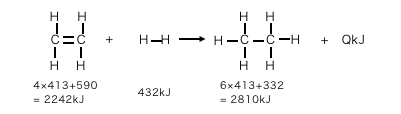
\(\mathrm{ Q = 2810 – (2242+432) }\)
\(\mathrm{ Q = 136kJ}\)
一旦全部バラバラにして再構成すると、
Qだけエネルギーが余るイメージです。
このようにみると、
熱化学方程式を「＝」で書く意味が見えてきますね。
③生成熱と反応熱
今回は少しイレギュラーなパターンです。
ただしエネルギー図の意味が理解できていれば、
今までの知識でも十分解くことができます。
\(\mathrm{ H_{2} + \frac{1}{2}O_{2} = H_{2}O(気) + 242kJ }\)
\(\mathrm{ NH_{3} + \frac{3}{4}O_{2} = \frac{1}{2}N_{2} + \frac{3}{2}H_{2}O(気) + 317kJ }\)
\(\mathrm{ N_{2} + O_{2} = 2NO – 180kJ }\)
\(\mathrm{ 4NH_{3} + 5O_{2} = 4NO + 6H_{2}O(気) + QkJ }\)
（解答）
求めたい生成熱をqとして、
単体、化合物、完全燃焼物のエネルギー図に、
アンモニアの生成反応を書き込みます。
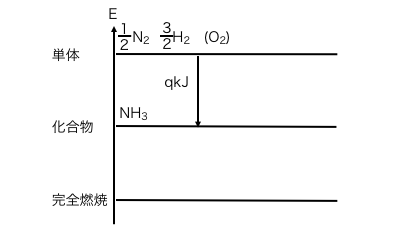
次に水素の燃焼反応を書きます。
しかし今回は窒素が燃焼しないことに注意です。
イレギュラーですが窒素は変化させずに移動させます。
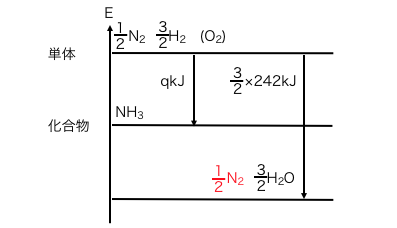
一瞬変な感じもしますが、
放出している熱と物質の変化が対応しているので、
本質的には問題ありません。
そして最後にアンモニアの燃焼です。
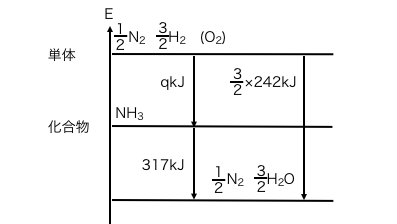
これを計算すれば、
\(\mathrm{ q + 317 = \frac{3}{2}\times242 }\)
\(\mathrm{ q = 46kJ}\)
次にQですが、
この反応はアンモニアからNOと水が生じます。
先ほどのアンモニアからN2と水が生じるのとは、
もちろんエネルギー的に違いますから、
図にもう一つエネルギーを作ってしまいます。
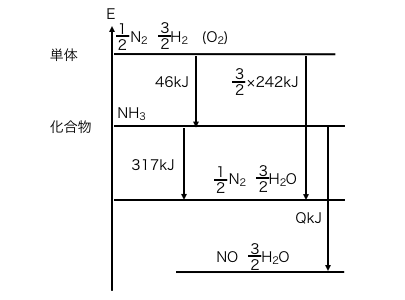
そして3つ目の式も書き込んでしまいます。
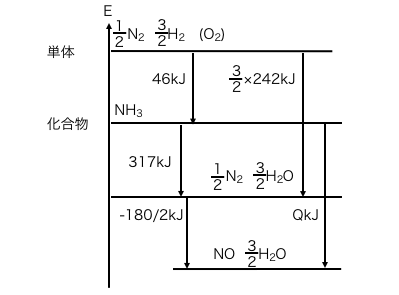
以上の図より、
\(\mathrm{ Q = 317 + (-\frac{180}{2}) }\)
\(\mathrm{ q = 227kJ}\)
最後の問題の補足
最後にエネルギー図の本質的なところを説明しておきます。
まだエネルギー図に慣れていない人は、
とりあえず①②や、手元の簡単な問題で慣れてから読んでください。
ある程度形式的に問題が解けるように、
エネルギーの６段階を基本に考えました。
しかし正確には、
例えば以下のような扱い方もできます。
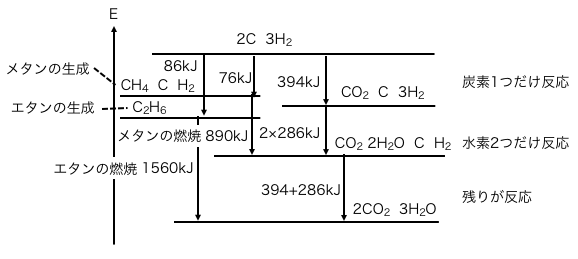
注意：
この図はただ数字遊びをしているだけで、
深い意味がある図ではありません。
ヘスの法則より、
反応熱は反応経路によらないから、
化学反応に対応した熱を書き込んでいけば、
自由にエネルギー図が書けるのです。
最初のうちはこの意味がわからなくていいので、
エネルギー図に慣れてきたらもう一度考えてみてください。
まとめ
今回は大ボリュームの記事でしたね。
この内容を理解するだけで、
熱化学方程式は得意分野になることでしょう。
エネルギー図を理解していれば、
仮に数式的に解こうとした場合でも、
解法の指針が明確に立つようになります。
逆にエネルギー図を知らないと、
闇雲に計算をして、間違えても理由がわからない、
という状態に陥ります。
ぜひ練習問題を通して、
きっちりと理解していってください。
