「理論化学って計算が大変だなあ…」
あなたもこんな印象を持っていませんか?
理論化学で計算が大変に思える理由の一つに、
「濃度の計算の複雑さ」が挙げられます。
日本中の高校生がこの濃度の計算で、
化学がわからなくなってしまうのです。
濃度計算がわからなくなってしまうのは、
濃度の正確な定義やイメージが理解できておらず、
さらには計算の「型」を理解していないからです。
今回は濃度の説明と、濃度計算の本質的な方法を解説していきます。
ここでの内容をしっかりと理解することで、
濃度の計算がスラスラと自動的にできるようになり、
理論化学が簡単な科目に見えてくるでしょう。
濃度計算は理論化学のみならず、
化学全体で重要になってきます。
濃度計算のスピードと正確さだけで、
センター・二次の全体の得点も大きく変わってきます。
ぜひ最後まで読んでみてくださいね。
目次 [hide]
高校化学のいろいろな濃度
高校化学では、
質量パーセント濃度・モル濃度・質量モル濃度
の3つの濃度を習います。
多くの高校生が濃度計算でつまづくのは、
これらの定義をきちんと覚えられていないからです。
まずは濃度の定義を覚えていくのが第一段階ですね。
濃度の定義を正確に理解するためには、
「溶媒・溶質・溶液」の意味を正確に理解する必要があります。
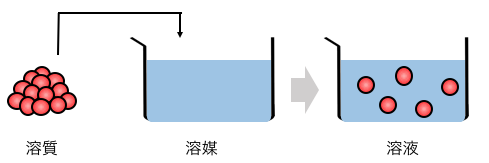
例えば塩水(NaCl水溶液)を例にとれば、
水が溶媒、そこに入れる塩が溶質、
それらを混ぜてできる塩水が溶液です。
ここから濃度の定義を見ていくのですが、
「溶媒・溶質・溶液」という言葉に注意して見ていきましょう。
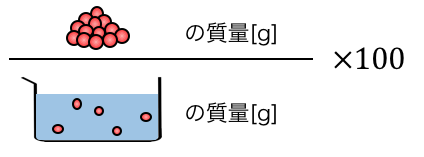
①質量パーセント濃度
\mathrm{ \frac{溶質の質量[g]}{溶液の質量[g]}×100[\%] }
「質量パーセント濃度」は、
溶液のグラムのうちの、どれだけが溶質のグラムかを
表した濃度です。
例えばクラスの中で男女の比率を考える時、
男子の比率は「男子の人数÷全員の人数」、
女子の比率は「女子の人数÷全員の人数」とすれば良さそうです。
このように一番単純に濃度を考えたのが、
質量パーセント濃度です。
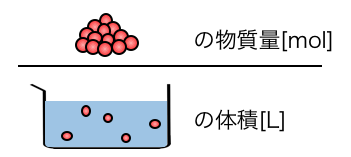
②モル濃度
\mathrm{ \frac{溶質の物質量[mol]}{溶液の体積[L]}[mol/L] }
「モル濃度」は、
溶液の体積の中に、溶質の粒がどれくらい溶けてるか、
を表した濃度です。
モル濃度のイメージは「人口密度」。
狭い部屋に人が集まれば人口密度が高いし、
広い部屋にちょっとしかいなければ人口密度が低いです。
このように、溶質の粒が、
どれくらいの密度で集まっているかを表したのが、
モル濃度なのです。
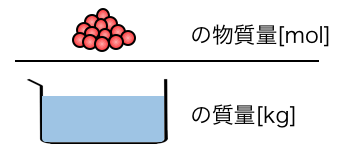
③質量モル濃度
\mathrm{ \frac{溶質の物質量[mol]}{溶媒の質量[kg]}[mol/kg] }
「質量モル濃度」は、
溶媒の質量に対して、どれだけの粒が溶けているか
を表す濃度です。
今までの濃度の分母が溶液だったのに対し、
今回の分母は溶媒になっていることに注意しましょう。
このように、1kgの溶媒に対し、
どれくらいの溶質の粒を溶かし込んだかが、
質量モル濃度なのです。
質量モル濃度は、溶かす溶質が2倍になれば濃度も2倍になります。このように定義しておくと後々便利です。
例えば「凝固点降下」では「溶かす溶質が2倍になると、2倍凝固点が下がる」という性質があるので、質量モル濃度を使って考えることができます。
濃度変換の方法
濃度の意味は理解できたでしょうか。
濃度の意味が理解できたら次は、
「濃度の変換」を考えていきましょう。
濃度変換は問題を解くときに何度も出てきますが、
結構苦手意識を持っている人も多いでしょう。
でも、きちんと濃度の意味さえ理解していれば、
濃度の変換は流れ作業でできるので、
そんなに怖がらなくても大丈夫です。
計算の仕方を順番に見ていきましょう。
化学計算のコツ
濃度の変換を考える前に、
化学計算のコツについて話します。
例えば以下の問題を見てみます。
(1)0.50molの水H2Oは何gか。
(2)8gの酸素O2は標準状態で何Lか。
(1)ではmolからgに単位を変換したいです。
molからgへの変換に使うのがモル質量。
H2O=18[g/mol]だから、以下のように考えることができます。
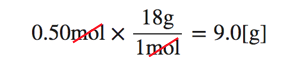
水は、0.50molも9.0gも同じ量を指していて、
この計算式はただ単位変換をしているだけなのです。
化学の計算の多くはこのように、
単に単位を変換しているだけのものが多いです。
(2)も同様に考えられます。
今回は最初にわかっている単位がgですが、
化学の基本はモルで考えることなので、
g→mol→Lの順で変換していきましょう。
O2=32、標準状態では1molの気体の体積は22.4Lだから、
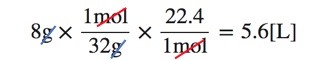
単位を変換していくと自然に答えにたどり着けるのです。
濃度変換の練習
それでは濃度変換の方法を見ていきます。
①質量パーセント濃度→モル濃度
98%濃硫酸(密度1.84g/cm3)のモル濃度は何mol/Lになるか。
まず、最初に確認しておきたいのが、
「濃度は体積に依存しない」ということです。
海の水を直接舐めようと、
海の水をコップですくって舐めようと、
しょっぱさは変わりませんね。
つまり濃度の変換を考えるときには、
自分の好きな量の溶液を持ってきて考えればいいのです。
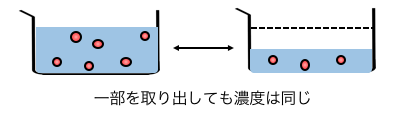
それでは濃度の変換です。
先ほども説明した通り、
化学計算の基本は単位の変換です。
今回の目標はmol/Lで、分母がLですから、
溶液1Lを持ってきたときのモル濃度を考えてみましょう。
モル濃度の分母は溶液の体積[L]ですから、
まずは以下のようになります。

次に分子です。
今持っている情報は溶液1Lだけですから、
これを溶媒の情報へ変えていきます。
溶液から溶媒の情報に変えるためには、
質量パーセント濃度が必要になりますが、
質量パーセント濃度の単位はg/gです。
そこでまずは溶媒1Lの単位をgに変換していきます。
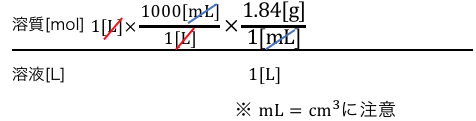
これで晴れて溶液ののgになりました。
質量パーセント濃度を使うことで溶質の情報に変換しましょう。
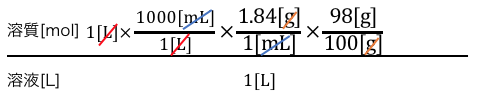
これで溶質のgになりました。
目標は溶質のmolでしたから、
H2SO4=98g/molを使えば、
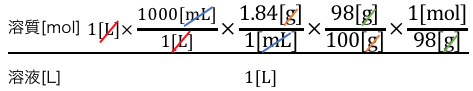
これによって単位が目標のmol/Lになりましたね。
最後に計算してあげれば答えが求まります。
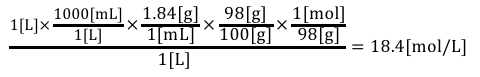
②質量パーセント濃度→質量モル濃度
20%グルコース水溶液(密度1.1g/cm3)の質量モル濃度は何mol/kgか(グルコースの分子量は180)。
こちらも同様に考えていきましょう。
目標はmol/kgですから、
まずは溶液1kgを持ってきたとしましょう。
分母は溶媒の質量kgですから、
質量パーセント濃度を用いて溶媒の質量に変換しましょう。
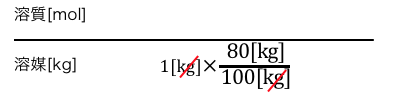
20%のグルコース水溶液ということは、
溶液の80%が溶媒であることを使いました。
これで分母は完成なので、次は分子です。
分母と同じように、
溶液の情報を溶質の情報に変えましょう。
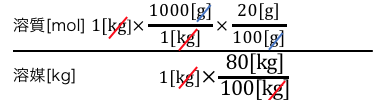
gをmolに変換したいので、
グルコースの分子量180g/molを使います。
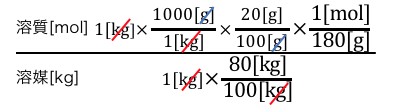
これで単位は揃ったので、
あとは計算するだけですね。
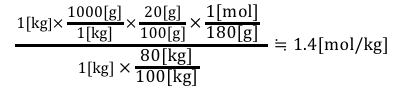
このように単位に注目すれば、
立式には困らないと思います。
ぜひマスターしてください。
まとめ
今回は濃度の定義と濃度計算の解説でした。
濃度には、
・質量パーセント濃度
・モル濃度
・質量モル濃度
の3種類がありましたね。
これらの定義は以下のようになっていました。
\mathrm{ \frac{溶質の質量[g]}{溶液の質量[g]}×100[\%] }
②モル濃度
\mathrm{ \frac{溶質の物質量[mol]}{溶液の体積[L]}[mol/L] }
③質量モル濃度
\mathrm{ \frac{溶質の物質量[mol]}{溶媒の質量[kg]}[mol/kg] }
まずはこの定義をきっちり覚えることが、
濃度計算で間違えないための第一歩です。
きっちり復習しておきましょう。
さらに濃度計算でのコツは、
モル計算と同様、単位を変換していくことでした。
これに関しては実際に自分でやってみて、
確認しておきましょう。














コメントを書く