体心立方格子、面心立方格子、六方最密構造。
これらはどれも入試頻出事項ですが、
きちんとその仕組みから理解できていますか?
「球体が中心だから体心!」
「面に中心がくるから面心!」
などという表面的な理解で終わっていませんか?
このような浅い理解では、
毎回テストごとに無駄に頭を使ってしまいますし、
少し難しい問題が出るとお手上げになってしまいます。
ここでは、金属結晶の結晶格子の解説をしますね。
ここの内容を理解すれば、
どんな難関大からひねった問題を出されても、
全く動揺せずに答えを導けるようになるでしょう。
深く理解するとはこういうことなのか、
と感じると思います。
それでは解説していきます。
目次
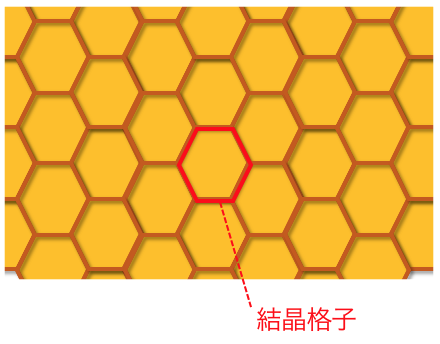
結晶格子とは
粒子どうしがなんらかの結合によって
規則正しくまとまったものが「結晶」です。
例えば六角形がたくさん集まることで、
蜂の巣ができているようなイメージです。

このような結晶において、
結晶の繰り返し単位のことを「結晶格子」といいます。
先ほどの蜂の巣の例で言えば六角形が結晶格子ですね。
金属結晶構造
まずは金属結晶の結晶格子を見ていきます。
金属結晶の結晶格子には、
・面心立方格子
・六方最密構造
・体心立方格子
の3種類があります。
これらの結晶格子のうち、
面心立方格子と六方最密構造は本質的には同じ原理でできています。
まずは原理を考えることで、
面心立方格子と六方最密構造を導いてみましょう。
面心立方格子・六方最密構造
もし粒子を敷き詰めて結晶を作るとしたら、
あなたならどう並べますか?
ボールを段ボールに詰め込むイメージです。
多くの人はできるだけたくさん詰まるように、
できるだけ隙間なく詰めるのではないでしょうか?
実はこの考え方でできている結晶が、
面心立方格子と六方最密構造です。
実際に粒子を詰め込んで結晶を作ってみましょう。
最密構造の作り方
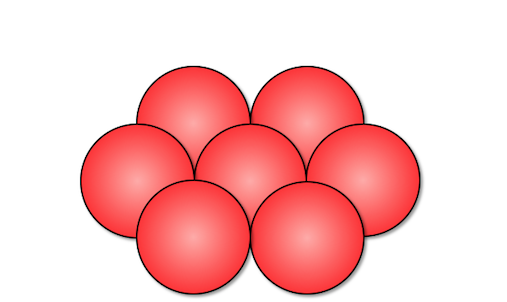
まずは1層目に綺麗に敷き詰めます。
これは想像通りでしょう。
では2層目を積み重ねるとどうなるでしょうか。
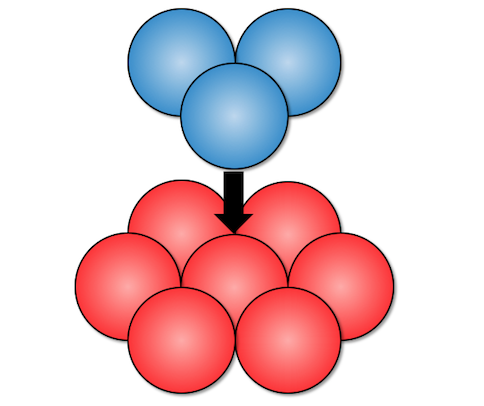
立体だとわかりづらいので、
一旦真上から見て考えましょう。
青い玉は、赤い玉が集まってできる、
くぼみのところにハマるはずですね。
そのくぼみは以下のように6つあります。
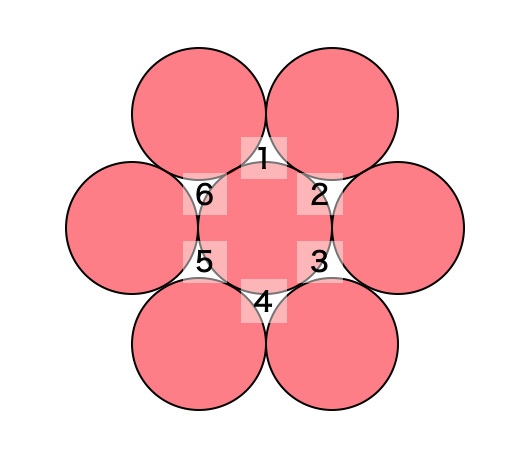
ということは、
135にハマる場合と246にハマる場合の
2種類が存在するということです。
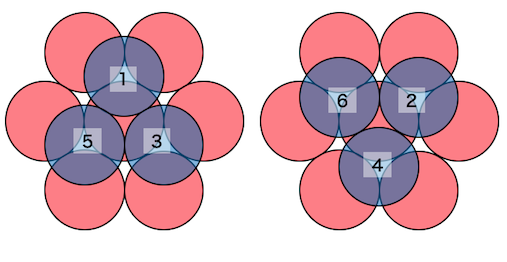
ただしこの2つは回転させれば全く一緒なので区別しません。
これによって2層目が詰め終わりました。
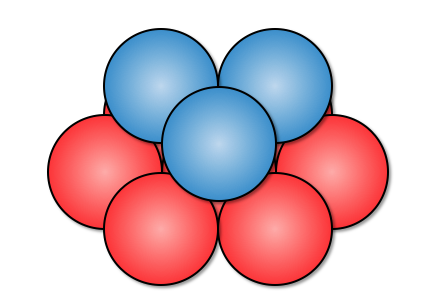
さて、ではいよいよ3層目です。
これも落ち着いて上からの図を見てみましょう。
すると今回は、
先ほどの135パターンと246パターンで、
異なる形になることがわかります。
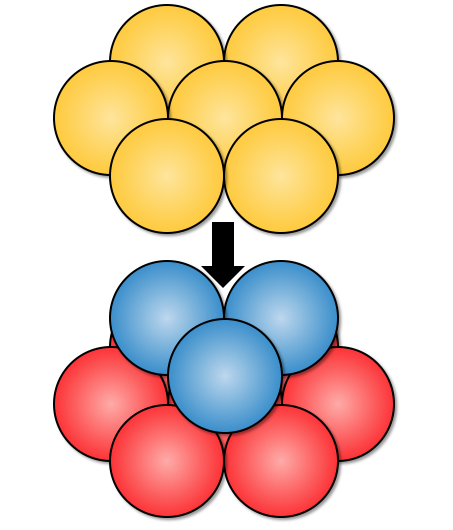
図の左側が「面心立方格子」、
図の右側が「六方最密構造」になります。
どちらも最密構造であることには変わりないということですね。
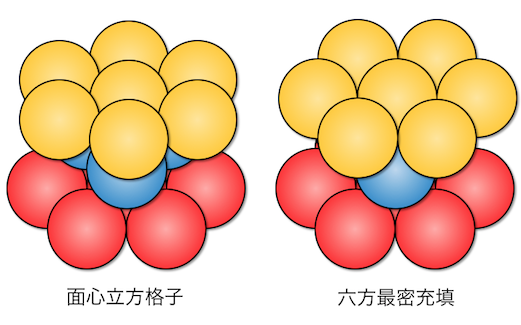
面心立方格子
先ほど面心立方格子を求めましたが、
いつも見る形ではありませんね。
そこでこれを少し傾けてみます。
すると以下のように、
いつもの面心立方格子が出てきます。
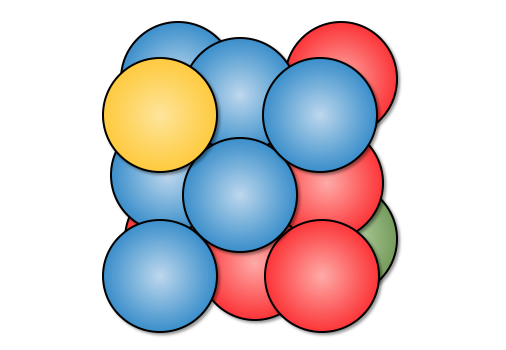
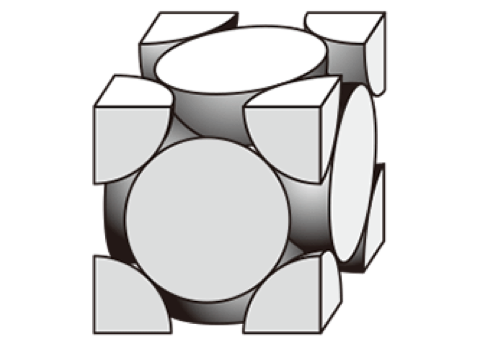
これの繰り返し構造のところだけを取り出せば、
以下のようになります。
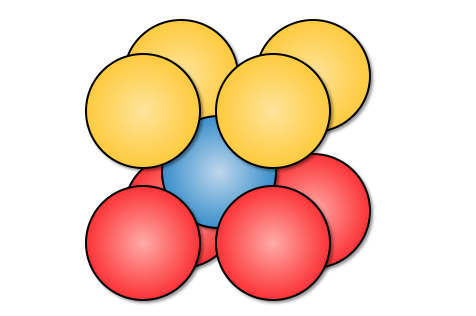
六方最密構造
六法最密構造は先ほどの図でわかりますね。
同様に繰り返し構造のところだけを取り出せば、
以下のようになります。
[画像13]
体心立方格子
最密充填でない金属結晶構造として、
「体心立方格子」があります。
先ほどとは違い、
それぞれの層どうしはぴったりくっついていますが、
層の中では隙間がありますね。
体心立方格子の繰り返し構造を取り出せば、
以下のようになります。
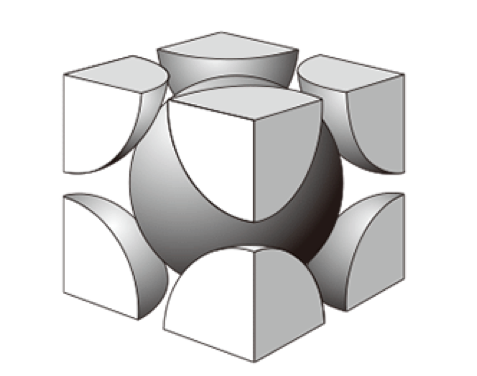
例えばダイヤモンドを思い出しましょう。ダイヤモンドは最密構造を取りたくても、結合の向きの関係で隙間ができています。金属でも「電子軌道」の関係で結合の向きが生じて、体心立方格子になることがあります。
(電子軌道を知りたい人はここをクリック!)
金属結晶の充填率
最後にそれぞれの結晶格子の「充填率」を求めてみましょう。
充填率とは、
箱の体積に対してどのくらい荷物が詰まっているか、
という値です。
結晶格子という箱の中で、
実際どれくらい原子が占めているか、
ということになります。
充填率を求める手順は、
①うまく断面積を考えて、
結晶格子の辺の長さと原子半径の関係を得る
②結晶格子内の原子数を数える
③結晶格子と原子の体積から充填率を求める
です。
それぞれの結晶格子で実際に求めてみます。
面心立方格子の充填率

「うまく断面積を考える」というのは、
結晶格子の辺と原子半径を含むような、
断面積を見つけるということです。
面心立方格子では、
結晶格子の壁面に注目すると良さそうです。
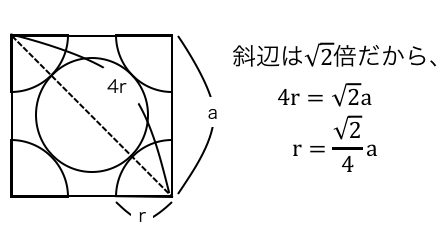
以上から1辺と半径の関係が得られました。
次にこの箱の中にいくつ原子があるか数えてみましょう。
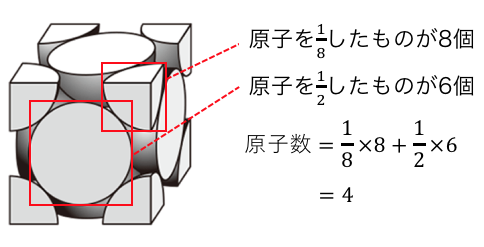
よって原子数は4つです。以上から、

このようにして、充填率が約74%とわかりました。
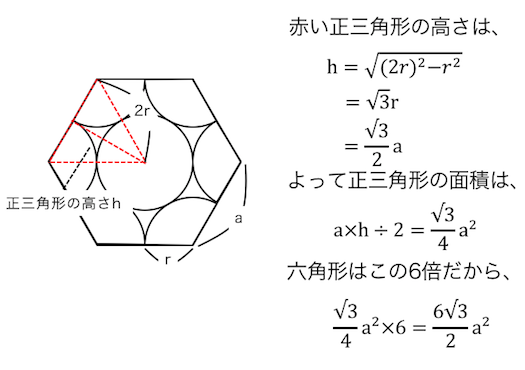
六方最密構造の充填率
[画像]
次に六方最密構造です。
①の手順として上下面に注目すれば、
辺と半径の関係が求まります。
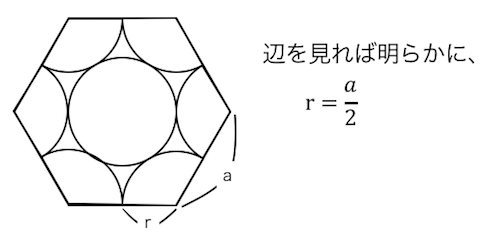
次に原子数を数えましょう。
[画像20]
よって原子数は6つです。
次に③ですが、
六方最密構造自体の体積が少しわかりづらいですね。
以下のようにすれば体積が求まります。
[画像22]
よって六方最密構造の充填率は、

面心立方格子と同じで最密になるようにしたのだから、
同じ74%になるのは当たり前ですね。
[画像]
ただ充填率を求めるだけなら、最小単位でなくても大丈夫です。
体心立方格子の充填率

先ほども説明した通り、
結晶格子の辺と原子半径を含むような、
断面積を見つけたいです。
単純に壁面だと辺上の2半径に隙間があり、
うまく式が立てられなさそうです。
そこで体心立方格子では、
対角線上に切った断面積を考えます。
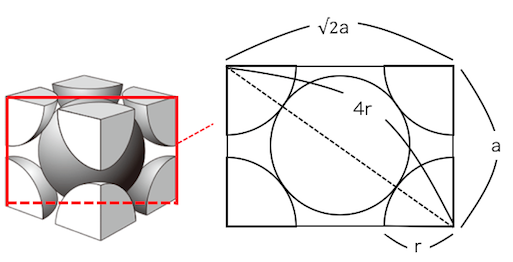
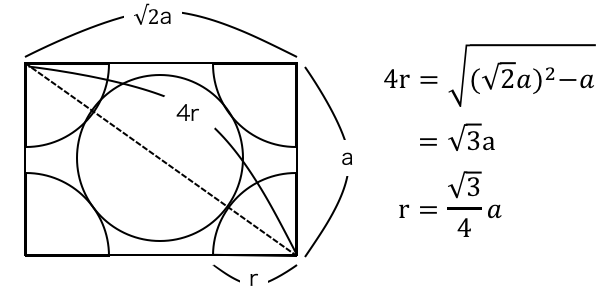
これでうまく計算できそうです。
以下のようにすれば辺と半径の関係が求まります。
次に原子数を数えてみましょう。
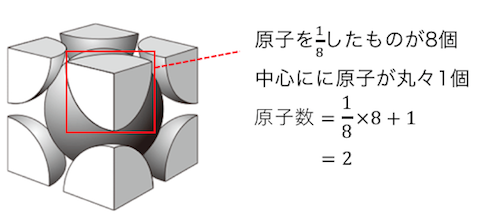
よって原子数は2つです。以上から、

壁面を見たときに2半径に隙間がありましたが、
やはり充填率も68%と小さくなっています。
まとめ
今回は金属結晶格子の解説でした。
金属の結晶構造には主に、
・面心立方格子
・六方最密構造
・体心立方格子
の3種類があり、面心立方格子と六方最密構造が最密な構造をとるのでした。
その理由も仕組みから考えれば問題ないでしょう。
結晶格子の問題は入試頻出で、
特に充填率周りの計算は必ずできる必要があります。
よく練習しておきましょう。














コメントを書く