混合気体の分圧はかなりの高校生がつまづく分野です。
「どこに目をつければいいかわからない!」
「そもそもこの計算なにやってるの?」
あなたも混合気体の分圧で、
頭の中がごちゃごちゃになっていませんか?
混合気体の分圧の問題で苦労してしまうのは、
気体が混ざるという「現象」を正しくイメージできていないからです。
ここでは混合気体の分圧を、
何が起こっているのかがイメージしやすいように解説します。
この記事を読むことで、
混合気体の動きが頭の中でイメージできるようになり、
解法に全く困ることなく問題を解けるようになります。
もはや「分圧って何が難しいの?」という状態になるでしょう。
それでは解説していきます。
気体を混合するとどうなるか
気体の性質を考えていくためには、
「気体の状態方程式」が必要不可欠です。
ぜひ以下も確認しておいてください。
かなり基本的な内容からお話しします。
物質量nAの気体Aが体積VAの箱の中に入っているとしましょう。
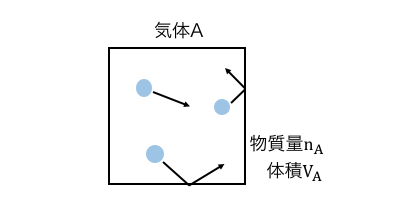
「体積」とは気体が動き回れる範囲のことですから、
このときの気体の体積はVAです。
それではこの気体Aの入った箱を、
物質量nBの気体Bが入った体積VBの箱とくっつけたらどうなるでしょう。
AとBの間の板を外すと、
気体Aの動ける範囲がVA+VB(=V)に広がります。
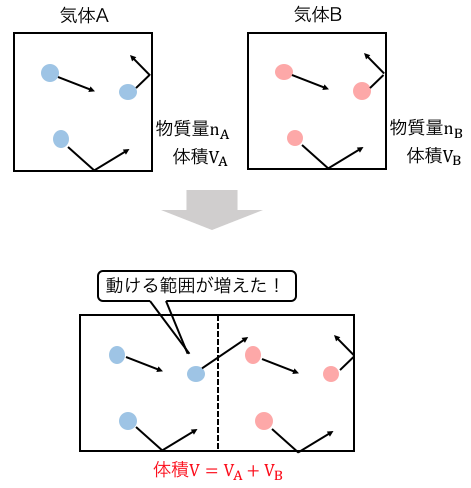
もちろん気体Bにも同じことが言えて、
壁を取り去ることで動ける範囲がVになりました。
今、気体たちは体積Vの箱の中にいて、
気体Aは圧力PAを、気体Bは圧力PBを、
箱全体にかけています。
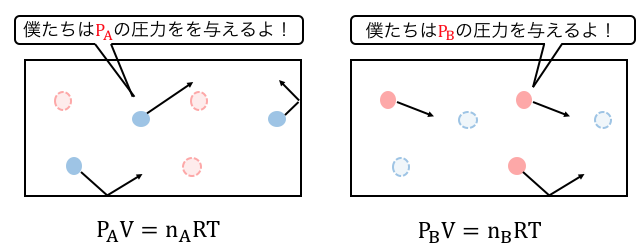
しかし気体の粒は外から見ると区別できず、
しかも気体Aと気体Bから同時に圧力を受けますから、
実質的には以下のようになります。
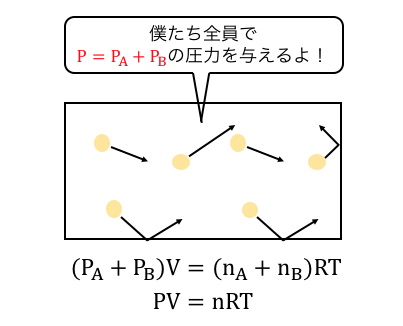
このように混合気体の中で、
個々の気体の圧力PA、PBのことを「分圧」といい、
混合気体の全体の圧力P=PA+PBを「全圧」といいます。
ドルトンの分圧の法則
以上の混合気体の性質を、
もう少しきちんとした流れで考え直しましょう。
以下のような混合気体があったとします。
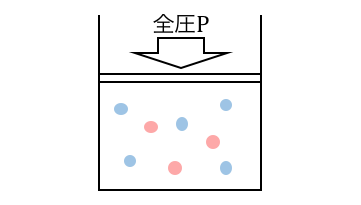
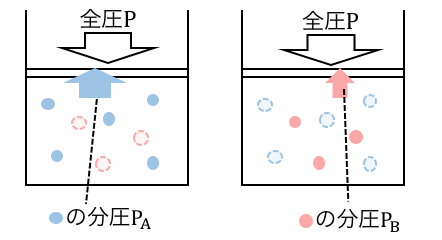
このときそれぞれの気体について、
もしも自分以外がいなかったときの圧力を「分圧」と言います。
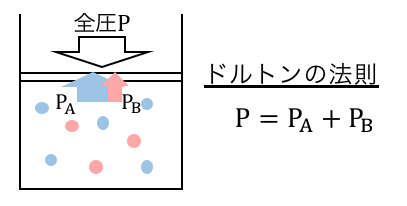
この「もしもの圧力」である分圧を全部足すと、
ちょうど全圧に一致します。
これを「ドルトンの分圧の法則」と言います。
分圧と全圧について状態方程式を考えれば、
\begin{align*}
\mathrm{ PV } &= \mathrm{ (n_{A}+n_{B})RT }\cdots① \\
\mathrm{ P_{A}V } &= \mathrm{ n_{A}RT }\cdots②\\
\mathrm{ P_{B}V } &= \mathrm{ n_{B}RT }\cdots③
\end{align*}
混合気体ではVとTが共通だから、
②と③からわかるように分圧と物質量の比が同じです。
さらに②÷①を考えれば、
\[
\mathrm{ P_{A} = P × \frac{n_{A}}{n_{A}+n_{B}} }
\]
のように全圧のモル分率が分圧となっています。
分子の粒の数だけ圧力を加えている、
という意味なので、これは当たり前ですね。
練習問題
分圧のイメージが湧いたところで、
いくつか練習問題を考えてみましょう。
(1)体積一定の容器に水素を0.2mol、酸素を0.3mol入れると全圧が1.0×105になった。それぞれの分圧は何Paか。
(2)体積8.3Lの容器に水素を0.5mol、酸素を0.4mol入れて27℃にした。全圧とそれぞれの分圧は何Paか。
すぐに公式を思い出そうとするのではなく、
どんな現象が起こっているのかをイメージしてみましょう。
そうすると自然に公式が思い浮かんできます。
それでは解説です。
(1)
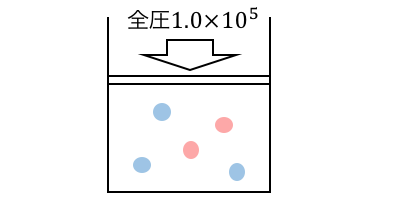
モル分率の公式を使えばいいのだけれど、この絵が頭に浮かべば「水素が2/5、酸素が3/5の圧力を担当するんだな」とイメージできますね。
\begin{align*}
P_{H_{2}} &= \frac{0.2}{0.2+0.3}×1.0×10^{5} \\
&= 4.0×10^{4} \\
P_{O_{2}} &= \frac{0.3}{0.2+0.3}×1.0×10^{5} \\
&= 6.0×10^{4}
\end{align*}
(2)
まずは全圧を出します。
\begin{align*}
P &= \frac{(0.5+0.4)×8.3×10^{3}×(27+273)}{8.3} \\
&= 2.7×10^{5}
\end{align*}
あとは先ほどと同じです。
\begin{align*}
P_{H_{2}} &= \frac{0.5}{0.5+0.4}×2.7×10^{5} \\
&= 1.5×10^{5} \\
P_{O_{2}} &= \frac{0.4}{0.5+0.4}×2.7×10^{5} \\
&= 1.2×10^{5}
\end{align*}
まとめ
今回は分圧の解説でした。
分圧とは自分以外がいなかったとした時の圧力で、
分圧を全て足すと全圧になるのでした。
このように一言にまとめると単純ですが、
一番大切なのは現象を正確に理解することです。
きっちりと現象をイメージできるまで、
しっかりと復習しましょう。














コメントを書く