沸点上昇・凝固点降下を解説！

沸点上昇・凝固点降下の解説です。

なんとなく溶液の分野というだけで、
苦手意識を持っている人が多いのではないでしょうか。

でも沸点上昇・凝固点降下は、
実はめちゃくちゃ簡単な分野です。

ここでミスってしまうのはもったいない。

この記事では仕組みから本質的に説明します。

ここの内容を理解しておけば、
沸点上昇・凝固点降下はもう忘れなくなります。

仕組みから理解すると、
忘れたくても忘れられなくなるのです。

ぜひ最後まで読んでみてください。

沸点上昇・凝固点降下とは

「沸点上昇」とは、
溶液に溶質を溶かすと沸点が上がる現象のことです。

同様に「凝固点降下」とは、
溶液に溶質を溶かすと凝固店が下がる現象のことです。

「上がったり下がったり、どっちなんだー！」
と思う人もいるかもしれませんが、
仕組みに注目すればこれは当然のことなんです。

では仕組みを見ていきましょう。

「邪魔者」のせいで沸点が上昇

液体は常に「気液平衡」の状態にあるのでした。

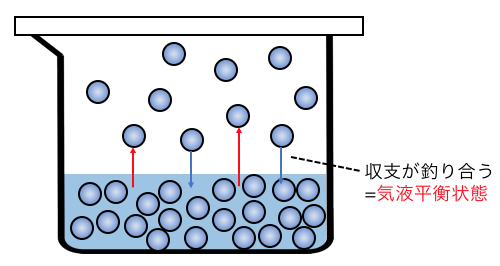
これに関しては以下の記事で解説しているので、
そちらをごらんください。

飽和蒸気圧とは？仕組みから徹底解説！

それではこのように気液平衡状態の水に、
例えば砂糖を溶かしたらどうなるでしょうか。

今まで自由に蒸発できていた水分子が、
砂糖という「邪魔者」によって蒸発を阻止されてしまいます。

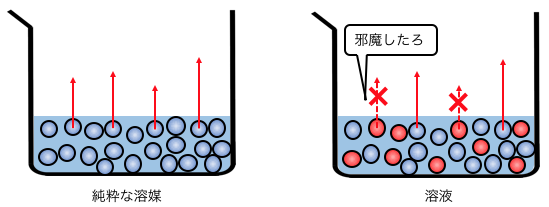
蒸発する力が弱まるのだから、
蒸気圧は小さくなりますよね。

これが「蒸気圧降下」です。

以下の蒸気圧曲線を見れば、
蒸気圧降下=沸点上昇だとわかりますね。

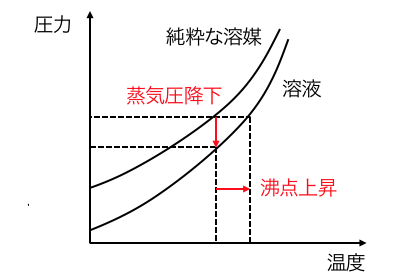
結局のところ、溶質という邪魔者のせいで、
沸騰に余計エネルギーが必要になるのが沸点上昇なのです。

凝固点降下も仕組みは同じ

凝固点降下も同じ仕組みです。

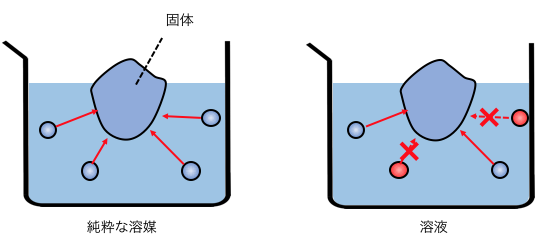
固体にぶつかる水が溶質に阻止されるため、
凝固するのに余計低い温度にする必要があるのです。

沸点上昇も凝固点降下も同じ仕組みですね。

沸点上昇度・凝固点降下度の計算

それでは、
実際に沸点上昇や凝固点降下において、
どのくらい沸点・凝固点が変化するのか見てみましょう。

沸点の上昇度を\(\Delta t_{b}\)、凝固点の降下度を\(\Delta t_{f}\)とすると、
溶質の種類に関係なく質量モル濃度\(m\)を使って表せます。

日本語に直すなら、
沸点上昇度は質量モル濃度に比例する
となりますね。

その比例定数をモル沸点上昇といい、
溶媒の種類によって決まります。

普段はモル濃度を使うことが多いですが、
今回は「質量モル濃度」であることに気をつけましょう。

質量モル濃度については以下もチェックしておいてください。

モル濃度・質量パーセント濃度・質量モル濃度！濃度計算のコツも解説！

計算の注意点

沸点上昇度や凝固点降下度は、
溶質の粒の数によって決まるのでした。

もし溶質が電解質で、
溶液中で電離してしまう場合は、
「邪魔者」が増えてしまいます。

よって溶質が電解質の場合は、
電離して粒が増えるのを考慮しないといけません。

仕組みを理解していれば、
「まあそうなりそうだな」と感じますね。

同じ理由で、
仮に溶質が「会合」するような場合は、
粒が減ることで温度変化も小さくなります。

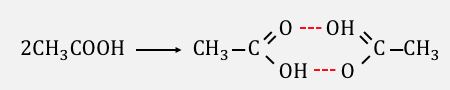
このような場合は、
「見かけの質量モル濃度」を考える必要があるので、
計算の際には注意しておきましょう。

練習問題

今回は理論の説明ばかりで計算をしていないので、
少しだけ練習問題を用意しておきます。

ぜひ自分で頭を使いながら解いてみてください。

まとめ

今回は沸点上昇、凝固点降下の説明でした。

溶媒に溶質という「邪魔者」が入ることで、
気体になったり固体になったりするのが邪魔され、
沸点や凝固点が変化するのでしたね。

そして温度変化は質量モル濃度に比例し、

で表されるのでした。

ぜひ練習問題も自力で解いてみてください。