ヘンリーの法則は実はめちゃくちゃ簡単なのに、
ほとんどの高校生が一度はつまづいてしまいます。
あなたもヘンリーの法則に出会った時に、
「何が起こってるんだー！？」
と思ったことがあるのではないでしょうか？
ヘンリーの法則がわからなくなるのは、
ヘンリーの法則の説明の仕方が2種類あり、
そのせいで現象のイメージが浮かばなくなるからです。
今回は「何が起こっているか」がイメージできるように、
ヘンリーの法則を解説します。
ここの内容をきちんと理解すれば、
ヘンリーの法則がめちゃくちゃ簡単な問題に見え、
気体の問題がスラスラ解けるようになります。
ぜひ最後まで読んでみてください。
ヘンリーの法則とは
「ヘンリーの法則」とは、
温度と溶媒の量が一定であれば、
溶媒に溶ける気体の物質量は圧力に比例するという法則です。
短い言葉で言えば、
押した分だけ溶ける
ということです。
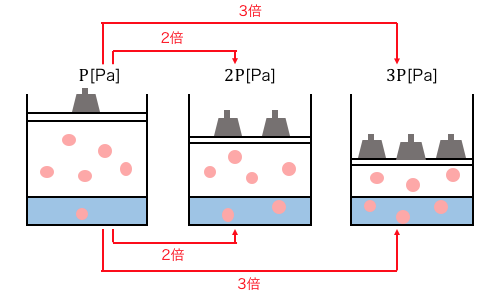
このように考えるとヘンリーの法則はとても単純です。
1.0×105Paで押して1mol溶けるのであれば、
2.0×105Paで押すと2mol溶ける、というだけですね。
しかしこんなに単純なのに、
かなり多くの受験生がヘンリーの法則でつまずいてしまいます。
なぜそのようなことが起こるのかというと、
実際の問題では「物質量と圧力の関係」ではなく、
「体積と圧力の関係」を問われることが多いからです。
これについて次の章で見ていきます。
【合わせてチェック】
・気体の状態方程式の使い方を徹底解説！
・混合気体の分圧を解説！仕組みがわかれば簡単！
混乱の原因
ヘンリーの法則で混乱する原因は、
先ほどの「物質量と圧力の関係」による定義の他に、
「体積と圧力の関係」による定義があるからです。
一定温度で一定の量の溶媒に対して、
(i)物質量と圧力の関係
溶媒に溶ける気体の物質量は、圧力に比例する。
(ii)体積と圧力の関係
溶媒に溶ける気体の体積は、その圧力のもとで一定になる。
「比例するのか一定になるのかどっち！？！？」
と混乱してしまいそうですね。
しかし冷静に考えてみれば、
実はこれらは全く同じことを言っているんです。
現象がイメージできればとっても簡単なので、
ここから集中して見ていきましょう。
2つの定義の意味
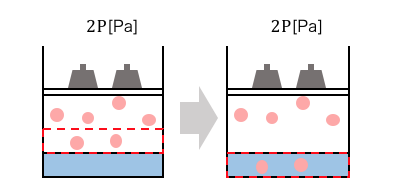
まずは圧力P[Pa]をかけたときに、
物質量n[mol]だけ溶けた場合を考えましょう。
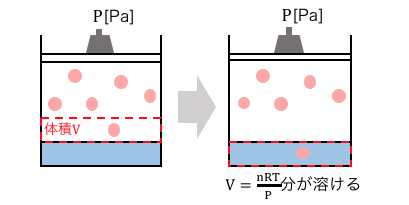
体積\(V=\frac{nRT}{P}\)分の気体が溶媒に溶け込んでいますね。
次に圧力を2倍の2P[Pa]にした場合です。
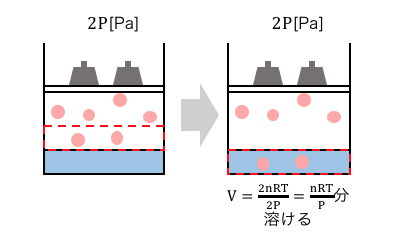
圧力を2倍にすることで、
先ほどの体積Vの場所に2n[mol]の気体が集まってきます。
これは\(V=\frac{2nRT}{2P}=\frac{nRT}{P}\)を考えれば、
わかりますね。
この体積Vの部分が溶け込むことによって、
2倍の物質量が溶媒に溶け込むことになります。
溶ける体積の量は一定だけども、
物質量は圧力に比例していることがわかりますね。
圧力が2倍であろうが3倍であろうが、
結局同じ仕組みで気体が溶けます。
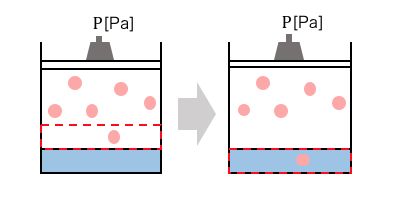
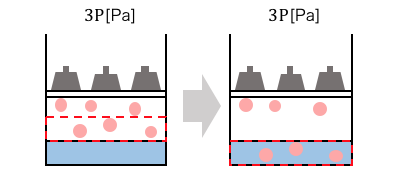
何が起こっているかがイメージできれば、
ヘンリーの法則はめちゃくちゃ簡単ですね。
さらに混乱を与える問題
実はヘンリーの法則がわからなくなる原因は、
もう1つあります。
例えば以下の問題を見てください。
1.0×105PaのCO2の水への溶解度は、水1.0Lに対して27℃で4.5×10-2molである。水1.0Lに対して27℃で2.0×105の圧力をかけると、その体積は1.0×105Paのもとで何Lか。
問題は最後の部分、
「その体積は1.0×105Paのもとで何Lか」
です。
これが何を表しているのかを順番に説明しますね。
まずは2.0×105PaでCO2を溶かします。
これまでに説明した通り、ヘンリーの法則に従って溶けます。
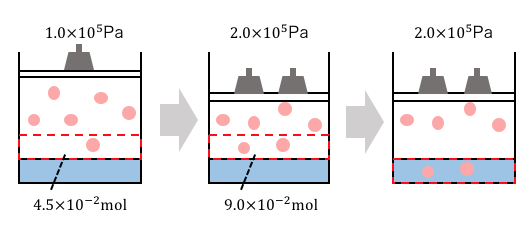
ここまでは先ほどの説明通りです。
しかし最終的に知りたいのは1.0×105Paのもとでの体積。
今の状態では2.0×105Paなので、
溶かした気体を仮に取り出してきたとすると、
それが1.0×105Paで何Lになるかをみる必要があります。
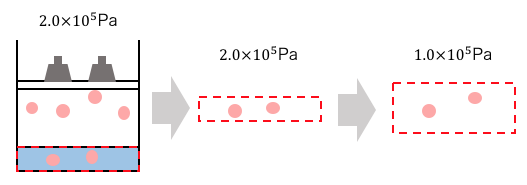
体積と圧力の関係によるヘンリーの法則では、
「その圧力のもとでは一定」となっていますが、
このように見る圧力が変わる場合には成り立たないのです。
圧力が2倍になっているから、溶ける気体の分子量はヘンリーの法則より、
\[
2×4.5×10^{-2}=9.0×10^{-2}mol
\]この物質量の気体の、1.0×105Paのもとでの体積は、
\begin{align*}
V&=\frac{9.0×10^{-2}×8.3×10^{3}×300}{1.0×10^{5}} \\
&=2.24…\\
&≒2.2[L]
\end{align*}
（解答2）
最初の状態で溶けている体積は、
\begin{align*}
\frac{4.5×10^{-2}×8.3×10^{3}×300}{1.0×10^{5}} \\
=1.12…\\
≒1.1[L]
\end{align*}ヘンリーの法則より、圧力を2倍にしても溶けている気体の体積は一定（物質量は変わっている）。
2.0×105Paのもとで1.1L溶けているのだから、1.0×105Paのもとでは、
\begin{align*}
2×1.12…\\
=2.24…\\
≒2.2[L]
\end{align*}
混合気体の場合
もし溶媒に接している気体が混合気体の場合も、
「分圧」で考えていくだけです。
具体的な問題で考えてみます。
混合気体で一見難しそうに見えますね。
でも分圧をしっかり理解していれば、
実は全然難しくないんです。
今、N2の分圧は0.8×105Paだから、
単に0.8×105PaのN2の溶解を考えればいいのです。
同様に、O2の分圧は0.2×105Paだから、
単に0.2×105PaのO2が溶けるのを考えるだけです。
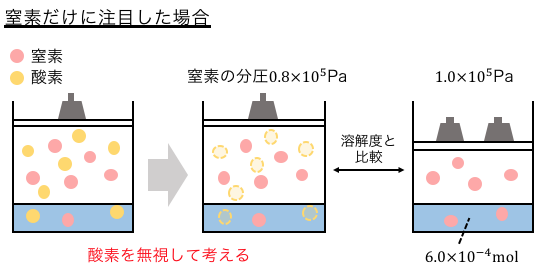
それでは解答を見てみましょう。
N2の分圧は0.8×105Pa。
1.0×105と比べると圧力は4/5倍で、
1.0×105での溶解度は6.0×10-4molだから、
\[
\frac{4}{5}×6.0×10^{-4}=4.8×10^{-4}mol
\]
O2の分圧は0.2×105Pa。
1.0×105と比べると圧力は1/5倍で、
1.0×105での溶解度は1.2×10-3molだから、
\[
\frac{1}{5}×1.2×10^{-3}=2.4×10^{-4}mol
\]
まとめ
今回はヘンリーの法則の解説でした。
ヘンリーの法則は、
「押したら溶ける」という単純な法則ながら、
定義の違いで混乱してしまうのでした。
押した分の粒がたくさん溶けるけど、
その分圧力で圧縮されるから体積は変化しない、
というのが理解できていれば混乱はしないでしょう。
さらにヘンリーの法則が理解できても、
問題形式や分圧が絡むことでややこしくなるので、
実際に問題演習も忘れずにやっておきましょう。
