気体の状態方程式の使い方を徹底解説！ │ 受験メモ

「ここではボイルの法則を使って…」

「次はシャルルの法則か…」

「状態方程式の計算、複雑すぎ…」

あなたも気体の問題で苦労していませんか？

気体の問題をすばやく正確に解くことは、
意外と難しいものです。

気体の問題をすばやく解くことができないのは、
気体の状態方程式の本質的な意味や、
その正しい使い方を理解していないからです。

ここでは気体の状態方程式の正しい考え方をお伝えします。

ここの内容を理解することで、
もう気体の問題で手が止まることはなくなり、
全く苦労せずに答えを導けるようになります。

気体の問題が早く解けることは、
センター試験・二次試験ともに大きなアドバンテージになります。

ボリュームのある記事ですが、
ぜひ読み飛ばさずに最後まで読んでみてください。

1 理想気体の状態方程式とは
2 状態方程式の使い方
3 参考：気体の混合
4 まとめ

理想気体の状態方程式とは

物質量n[mol]の気体が、圧力P[Pa]、絶対温度T[K]で、
体積V[L]を占めるとき、以下の「状態方程式」を満たします。

\[
\mathrm{ PV=nRT }
\]

Rは「気体定数」と呼ばれる比例定数です。

ここで、標準状態（0℃=273K、1.01×10⁵Pa）では、
どの気体も1molで22.4Lを占めるのでしたね。

これを代入すると気体定数を求めることができます。

\begin{align*}
\mathrm{R} &= \mathrm{\frac{PV}{nT}} \\
&= \mathrm{\frac{1.01×10^{5}×22.4}{1×273}} \\
&≒ \mathrm{8.3×10^{3}}
\end{align*}

どんな気体であっても、
いつも同じ式が成り立つというのは便利ですね。

しかし実際に計算をしようとすると、
P、V、n、Tと変数が多すぎて頭がごちゃごちゃになってしまいます。

だから問題を解くときにはちょっとした工夫をする必要があります。

状態方程式の使い方を理解して、
気体の問題がスラスラ解けるようになりましょう。

状態方程式は「理想気体」でしか成り立ちませんし、逆に言えば状態方程式PV=nRTを満たす気体のことを理想気体と言います。特別に「実在気体」が問われなければ、入試レベルではすべて理想気体だと思って良いでしょう。

状態方程式の使い方

例えば以下のような単純な問題があったとしましょう。

（問題）
27℃、6.0×10⁴Paで、0.20molの気体の体積は何Lか。

このような場合は単純に状態方程式を利用できます。

（解答）
\begin{align*}
\mathrm{V} &= \mathrm{\frac{0.20×8.3×10^{3}×(273+27)}{6.0×10^{4}}} \\
&= \mathrm{8.3[L]}
\end{align*}

しかし多くの場合は、
「体積を1Lから2Lへ変化させたとき、…」
「温度を27℃から77℃へ変化させたとき、…」
というように「変化」が起こるはずです。

このような場合は、
変化の前後の関係を考えることで、
状態方程式を効率良く利用できます。

いくつかの具体例で確認してみましょう。

①n、Tが一定の場合

（問題）
1.0×10⁵Paで体積が2.0Lの気体を、温度を変えずに4.0×10⁵Paに変化させたときの体積は何Lか。

この問題の場合、
変化の前後で物質量nと温度Tが一定です。

つまり状態方程式を以下のように見ることができます。

\[
\mathrm{PV=nRT=(一定)}
\]

つまり圧力P₁、体積V₁の状態から
圧力P₂、体積V₂の状態へ変化させたとき、
その前後でnとTが一緒なら以下のようになるということです。

\[
\mathrm{P_{1}V_{1}=P_{2}V_{2}}
\]

これを使って問題を解いてみましょう。

（解答）
n、Tが一定だから、
\begin{align*}
\mathrm{1.0×10^{5}×2.0} &= \mathrm{4.0×10^{5}×V} \\
\mathrm{V} &= \mathrm{0.50[L]}
\end{align*}

PV=(一定)であることを、「ボイルの法則」とも言います。しかしこのように状態方程式から導けるので、覚える必要は全くありません。

②P、nが一定の場合

（問題）
圧力一定で、27℃で体積3.0Lの気体を77℃まで温めると、体積は何Lか。

この問題の場合は、
物質量nと圧力Pが一定ですね。

つまり先ほどと同じように考えれば以下のようになります。

\[
\mathrm{\frac{V}{T}=\frac{nR}{P}=(一定)}
\]

よって変化の前後で、

\[
\mathrm{\frac{V_{1}}{T_{1}} = \frac{V_{2}}{T_{2}}}
\]

が成り立ちます。

これを「シャルルの法則」と言いますが、
先ほど同様覚える必要はないです（むしろ覚えてはいけません）。

（解答）
P、nが一定だから、
\begin{align*}
{\frac{3.0}{273+27}} &= \mathrm{\frac{V}{273+77}} \\
\mathrm{V} &= \mathrm{3.5[L]}
\end{align*}

「変化の前後で一定」とは、変化の間は全く無視して最初と最後だけを見ればいいということです。普通入試問題では「ゆっくりと変化させる」と書かれているので、変化の間は無視できるのです。「ゆっくりじゃない場合は？」と疑問に思う人は物理の「熱力学」の分野を勉強してみましょう。

③P、Tが一定の場合

（問題）
標準状態において、0.25molの気体の体積は何Lか。

以下で「モル計算」をマスターしているあなたなら、
この問題は一瞬で解けるでしょう。

モル計算を完全攻略！物質量なんて超簡単！

しかしここでは状態方程式の練習としてこの問題を解いてみます。

標準状態で1molの気体の体積は22.4Lでした。

同じ標準状態で0.25molの気体を考えたいのだから、
今回はPとTが一定になっています。

よって以下の通りです。

\begin{align*}
\mathrm{\frac{V}{n}} &= \mathrm{\frac{RT}{P} = (一定)} \\
\mathrm{\frac{V_{1}}{n_{1}}} &= \mathrm{\frac{V_{2}}{n_{2}}}
\end{align*}

これは「アボガドロの法則」を表していますね。

（解答）
P、Tが一定だから、
\begin{align*}
\mathrm{\frac{22.4}{1.0}} &= \mathrm{\frac{V}{0.25}} \\
\mathrm{V} &= \mathrm{5.6[L]}
\end{align*}

④V、nが一定の場合

（問題）
27℃で圧力が6.0×10⁴Paとなっている気体を、体積を変えずに77℃まで温めたときの圧力は何Paか。

今までと同じパターンなので迷うことはないでしょう。

Vとnが一定だから、

\begin{align*}
\mathrm{\frac{P}{T}} &= \mathrm{\frac{nR}{V} = (一定)} \\
\mathrm{\frac{P_{1}}{T_{1}}} &= \mathrm{\frac{P_{2}}{T_{2}}}
\end{align*}

（解答）
V、nが一定だから、
\begin{align*}
\mathrm{\frac{6.0×10^{4}}{273+27}} &= \mathrm{\frac{P}{273+77}} \\
\mathrm{P} &= \mathrm{7.0×10^{4}[Pa]}
\end{align*}

今までと違って「〜の法則」と呼ばれる名前はありませんが、どれも状態方程式を用いて考えただけですね。

参考：Tが一定の場合

（問題）
風船に0.050molの気体を入れて1.0Lにすると圧力が1.5×10⁵Paとなった。風船にさらに0.050mol気体を追加すると体積は1.5Lになった。風船内部は常に室温と同じだとすると、圧力は何Paか。

2倍の物質量の気体を入れた
ら体積も2倍になりそうですが、
風船はゴムの力で反発してきます。

これによって体積は2倍よりも小さくなり、
その分圧力が高まりますね。

このように定数が1つになってももちろん考え方は同じです。

\begin{align*}
\mathrm{\frac{PV}{n}} &= \mathrm{nR = (一定)} \\
\mathrm{\frac{P_{1}V_{1}}{n_{1}}} &= \mathrm{\frac{P_{2}V_{2}}{n_{2}} }
\end{align*}

（解答）
Tが一定だから、
\begin{align*}
\mathrm{\frac{1.5×10^{5}×1.0}{0.050}} &= \mathrm{\frac{P×1.5}{0.10}} \\
\mathrm{P} &= \mathrm{2.0×10^{5}[Pa]}
\end{align*}

もちろんPV/n=(一定)に名前はありません。

いつも状態方程式を型通り使うだけですね。

参考：気体の混合

この記事では最初から最後まで、
変化の前後に注目して状態方程式を使う
といってきました。

しかし以下のような場合は、
前後の状態が何を指すかに注意が必要です。

（問題）
体積2.0Lの容器Aにはアルゴンを圧力1.2×10⁵になるように入れ、体積4.0Lの容器Bには窒素を圧力1.8×10⁵になるように入れた。中央のコックを開けて充分時間が経ったときの、全体の圧力は何Paか。

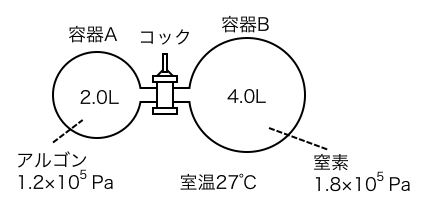
勘がいい人は「分圧の問題か」と気づくかもしれませんね。

変化の前後とはあくまで1つの気体に対してで、
2つの気体を同時に考えることはできません。

そのため気体ごとに分けて考える必要があります。

（解答）
コックを開けた後のアルゴンの分圧P_アルゴンは、
\begin{align*}
\mathrm{1.2×10^{5}×2.0} &= \mathrm{P_{アルゴン}×6.0}\\
\mathrm{P_{アルゴン}} &= \mathrm{0.40×10^{5}}
\end{align*}窒素の分圧P_窒素は、
\begin{align*}
\mathrm{1.8×10^{5}×4.0} &= \mathrm{P_{窒素}×6.0}\\
\mathrm{P_{窒素}} &= \mathrm{1.2×10^{5}}
\end{align*}以上から全体の圧力Pは、
\begin{align*}
\mathrm{P} &= \mathrm{P_{アルゴン}+P_{窒素}}\\
&= \mathrm{1.6×10^{5}}
\end{align*}

この問題をより深く理解するためには「分圧」を知っておく必要があります。ぜひ以下も読んでみてください。
【合わせてチェック】
・混合気体の分圧を解説！仕組みがわかれば簡単！