電離平衡とは？pHの求め方を解説！ │ 受験メモ

今回は電離平衡の解説です。

電離平衡は入試で難問として出題されやすいです。

多段階電離、塩の加水分解、緩衝液などなど
複雑な問題は本当に練習が必要です。

ここではそんな難しい問題に入る前に、
まずは電離平衡の基礎を確実にしておきましょう。

練習問題も用意しているので、
すでに授業で習った人も小手調べに解いてみてください。

それでは解説を始めます。

1 電離平衡とは
2 電離定数・電離度とは
- 2.1 電離定数の定義
- 2.2 電離度・電離定数の関係
3 練習問題
4 参考①：塩の加水分解
5 参考②：緩衝液
6 まとめ

電離平衡とは

電離平衡の基本の仕組みは、
今までやってきた平衡状態と同じ考え方です。

まだ平衡とはなにかが曖昧な人は、
ぜひ以下を読んでみてください。

絶対にわかる化学平衡の仕組み

「電離平衡」とはその名の通り、
ある物質の一部だけが電離して、
以下のような平衡状態を作ることを指します。

\[ \mathrm{ CH_{3}COOH + H_{2}O ⇆ CH_{3}COO^{-} + H_{3}O^{+} }\]

電離しようとする力と、
電離を阻止しようとする力が、
せめぎあっている状態です。

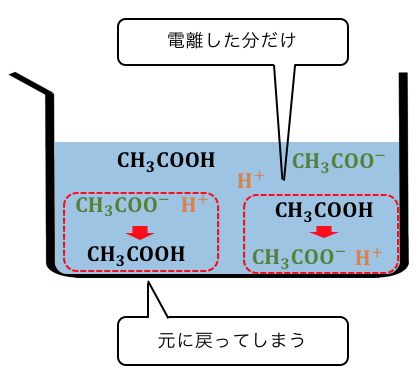
これは酸の例ですが、
当然塩基でも同じように電離平衡を起こすものがあります。

\[ \mathrm{ NH_{3} + H_{2}O ⇆ NH_{4}^{+} + OH^{-} } \]

電離定数・電離度とは

化学平衡を考えるときには、
「平衡定数」を考えました。

電離平衡の場合は代わりに「電離定数」を考えます。

順番に確認していきましょう。

電離定数の定義

\[ \mathrm{ CH_{3}COOH + H_{2}O ⇆ CH_{3}COO^{-} + H_{3}O^{+} }\]

電離「平衡」というくらいですから、
電離平衡でも平衡定数を考えることができます。

\[
\mathrm{ K = \frac{[CH_{3}COO^{-}][H_{3}O^{+}]}{[CH_{3}COOH][H_{2}O]}}
\]

ここで少し考えてみてください。

今は電離を考えているんだから、
いつだってH₂Oが関わってきます。

毎回H₂Oを書くのはめんどうですよね。

さらに水は溶質に加えて大量にあって、
水のモル濃度はめちゃでかいです。

だから水は一定だとみなし、
平衡定数と合わせて定数にしてしまいます。

\[
\mathrm{ K[H_{2}O] = \frac{[CH_{3}COO^{-}][H_{3}O^{+}]}{[CH_{3}COOH]}}
\]

定数であるK[H₂O]をまとめてK_aとおき、
H₃O^{+}をH^{+}で表すと以下のようになります。

\[
\mathrm{ K_{a} = \frac{[CH_{3}COO^{-}][H^{+}]}{[CH_{3}COOH]}}
\]

このように定義したK_aを「酸の電離定数」と言います。

塩基でも同様に考えてみましょう。

\[ \mathrm{ NH_{3} + H_{2}O ⇆ NH_{4}^{+} + OH^{-} } \]

定数であるK[H₂O]をまとめてK_bとおくと以下のようになります。

\[
\mathrm{ K_{b} = \frac{[NH_{4}][OH^{-}]}{[NH_{3}]}}
\]

このように定義したK_bを「塩基の電離定数」と言います。

酸も塩基も、
この電離定数が一定になるように、
反応が進行するのです。

1Lの水のモル濃度は、
\begin{align*}
\mathrm{ [H_{2}O] } &= \mathrm{ \frac{1000g}{1L} } \\
&= \mathrm{ \frac{1000g\times\frac{1mol}{18g}}{1L} } \\
&≒ \mathrm{ 55.6mol/L }
\end{align*}よってこのうちのほんの一部がH₃O⁺になってもほとんど影響がないのです。

電離度・電離定数の関係

電離平衡状態にある物質が、
どの程度の割合電離するかを表すのが「電離度」です。

この電離度を使って電離定数を計算してみましょう。

酢酸がC[mol/L]、電離度がαのとき、
各物質の量は以下のようになります。

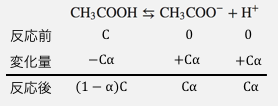
最初用意されていた酢酸のうち、
電離度が掛け算されたCα分だけが電離したのですね。

これらを先ほどの式に代入すると以下の通り。

\begin{align*}
\mathrm{ K_{a} } &= \mathrm{ \frac{[CH_{3}COO^{-}][H^{+}]}{[CH_{3}COOH]} } \\
&= \mathrm{ \frac{Cα\times Cα}{C(1-α)} } \\
&= \mathrm{ \frac{Cα^{2}}{1-α} }
\end{align*}

そして酢酸の電離度はかなり小さいので、
1-α≒1と近似すると以下のような関係が得られます。

\begin{align*}
\mathrm{ K_{a} } &≒ \mathrm{ \frac{Cα\times Cα}{C(1-α)} } = \mathrm{Cα^{2}}\\
\mathrm{ α } &= \mathrm{ \sqrt{\frac{K_{a}}{C}} } \\
\mathrm{ [H^{+}] } &= \mathrm{ Cα = \sqrt{CK_{a}} }
\end{align*}

普通酢酸の濃度Cと電離定数K_aは与えられますから、
酸のpHを求めるのに必要な[H⁺]が求まりそうですね。

以上の計算は弱塩基であるアンモニアも同様です。

アンモニアの濃度をC、電離度をα、電離定数をK_bとすると、

\begin{align*}
\mathrm{ K_{b} } &≒ \mathrm{ \frac{Cα\times Cα}{C(1-α)} } = \mathrm{Cα^{2}}\\
\mathrm{ α } &= \mathrm{ \sqrt{\frac{K_{b}}{C}} } \\
\mathrm{ [OH^{-}] } &= \mathrm{ Cα = \sqrt{CK_{b}} }
\end{align*}

練習問題

一度自分で手を動かしてみることも大切です。

練習問題を用意しておくので、
ぜひ解いてみてください。

水のイオン積を10^-14、log₁₀2=0.30とするとき、以下の問いに答えよ。
（１）酢酸の電離定数が2.0×10^-5であるとき、0.20mol/L酢酸水溶液のpHはいくつか。
（２）アンモニアの電離定数が1.0×10^-5であるとき、0.025mol/Lアンモニア水溶液のpHはいくつか。

（解答）
（１）復習の意味で、
もう一度電離定数と水素イオン濃度の関係を
導出しておきましょう。

1-α≒1に注意すると、

\begin{align*}
\mathrm{ K_{a} } &= \mathrm{ \frac{[CH_{3}COO^{-}][H^{+}]}{[CH_{3}COOH]} } \\
&= \mathrm{ \frac{Cα\times Cα}{C(1-α)} } \\
&= \mathrm{ \frac{Cα^{2}}{1-α} } \\
&= \mathrm{ Cα^{2} }
\end{align*}よって、
\begin{align*}
\mathrm{ α } &= \mathrm{ \sqrt{\frac{K_{a}}{C}} } \\
\mathrm{ [H^{+}] } &= \mathrm{ Cα = \sqrt{CK_{a}} }
\end{align*}これを用いれば、
\begin{align*}
\mathrm{ [H^{+}] } &= \mathrm{\sqrt{0.20\times 2.0\times 10^{-5}} } \\
&= \mathrm{ 2.0\times 10^{-3} }
\end{align*}よって求めるpHは、
\begin{align*}
\mathrm{ pH } &= \mathrm{ -log_{10}[H^{+}] } \\
&= \mathrm{ -log_{10}(2.0\times 10^{-3}) } \\
&= 2.7
\end{align*}

（２）こちらはいきなり公式を使ってしまいます。
\begin{align*}
\mathrm{ [OH^{-}] } &= \mathrm{\sqrt{0.025\times 1.0\times 10^{-5}} } \\
&= \mathrm{ 5.0\times 10^{-4} }
\end{align*}ここで少しテクニック。
pHではなく、pOHからもpHを計算できます。
\begin{align*}
\mathrm{ pOH } &= \mathrm{ -log_{10}[OH^{-}] }\\
&= \mathrm{ -log_{10}(5.0\times 10^{-4}) } \\
&= 4-\mathrm{ log_{10}5 }\\
&= 4-\mathrm{ (1-log_{10}2) }\\
&= 3.3
\end{align*}水のイオン積より、pH+pOH=14だから、pH=14-3.3=10.7。