今回は浸透圧の解説です。
高校生・受験生の多くは、
溶液の分野を苦手に思っています。
そのせいで浸透圧にも、
なんとなく苦手意識を持っている人も多いでしょう。
浸透圧がなんとなくわからないと思っている人は、
「浸透圧」がなんの圧力を指しているのかが、
曖昧になっていることが多いです。
今回は浸透圧をきちんと定義から復習し、
本質的に理解していきましょう。
そうすることで、
もう浸透圧に対しての苦手意識もなくなり、
すぐに得点源にできると思います。
それでは解説を始めます。
浸透とは

料理をするときに、
野菜を塩もみしたり、肉や魚に味付けしたりすると、
食材から水が出てくると思います。
この現象を「浸透」といいます。
それではこの現象の原理を見てみましょう。
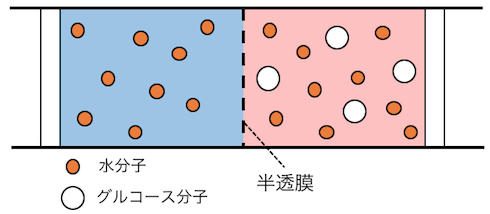
このように、
2つの液体を用意します。
そして「小さい分子は通すけど大きい分子は通さない」
という性質を持った「半透膜」で区切ります。
そうすると半透膜の穴を通れる分子だけが、
左右を行き来しますね。
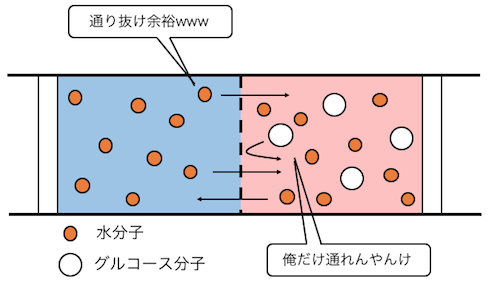
水分子は好きに通れるけど、
グルコース分子はチャレンジはするものの跳ね返されます。
これによって、
水分子100%の左側の液体が、
右側にどんどん流れ込みます。
このような現象を「浸透」と言います。
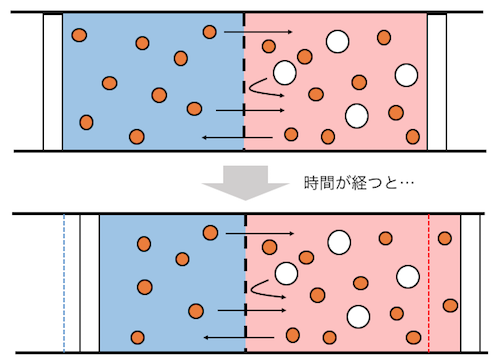
右側の濃い溶液を薄めるような方向に、
水が流れていくのですね。
先ほど例に挙げた肉や野菜も、
味付けをして外側の濃度が高くなったことで、
水が外に出てきたのです。
浸透圧とは
それでは次に「浸透圧」を説明します。
浸透圧とはその名の通り、
「浸透するときの圧力」のことです。
ただこれだと少し分かりづらいので、
もう少し細かく見ていきましょう。
浸透圧の定義
浸透が起こると先ほどのように、
濃い溶液側の溶媒が増えていきます。
これを力で押さえ込んで、
水が浸透してこないようにしてみます。
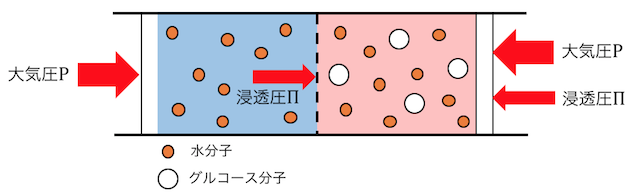
このようにすると、
半透膜を超えて水が浸透しようとする圧力と、
溶液の上から押さえ込もうとする圧力が釣り合います。
このときの圧力のことを「浸透圧」といいます。
つまり浸透圧とは、
・浸透してこようとする圧力
であり、
・浸透を押さえ込むために必要な圧力
でもあります。
浸透圧の計算方法
浸透圧を計算するための法則が、
「ファントホッフの法則」です。
浸透圧Πは、溶液のモル濃度Cと絶対温度に比例し、以下の関係となる。
\[
\mathrm{Π=CRT}
\]
これに関しては基本的には覚えるしかないですが、
少しでも暗記を減らすために以下のように考えてみます。
溶液の体積をV、溶質の物質量をnとすると、
モル濃度C=n/Vになることに注意すると、
\begin{align*}
\mathrm{Π} &= \mathrm{\frac{n}{V}RT} \\
\mathrm{ΠV} &= \mathrm{nRT}
\end{align*}
これは理想気体の状態方程式と全く同じ形ですね。
これを覚えておくと、
浸透圧の式自体はもう忘れないと思います。
次の章に練習問題を用意しておくので、
あとは具体的な問題を解きながら公式を理解していきましょう。
\[ \mathrm{ΠV = \frac{w}{M}RT}
\]この式を使って、浸透圧からモル質量を求める場合もあります。
練習問題
ただ式を見ただけでは問題は解けるようになりません。
今回は2つ練習問題を用意しておくので、ぜひチャレンジしてみてください。
問題1
まずは一番単純な問題から。
それでは解いてみましょう。
ファントホッフの式を思い出しましょう。
求める浸透圧をΠとおくと、
\begin{align*}
\mathrm{ ΠV } &= \mathrm{ nRT } \\
\mathrm{ Π\times 0.83 } &= \mathrm{ 0.050\times 8.3\times 10^{3}\times 300 } \\
\mathrm{ Π } &= \mathrm{ 1.5\times 10^{5}Pa }
\end{align*}
問題2
浸透圧はこのように、
有機化学の問題で分子量を求めるときに、
利用されることもあります。
試験本番で見たときにびっくりしないように、
一度練習しておきましょう。
分子量をMとしたとき、タンパク質w[g]の物質量nは、
\[n=\frac{w}{M}
\]であることに注意する。
条件をファントホッフの式に代入して、
\begin{align*}
\mathrm{ ΠV } &= \mathrm{ nRT } \\
\mathrm{ ΠV } &= \mathrm{ \frac{w}{M}RT } \\
\mathrm{ 3.0×10^{2}\times 0.83 } &= \mathrm{ \frac{4.0}{M}\times 8.3\times 10^{3}\times 300 } \\
\mathrm{ M } &= \mathrm{ 4.0\times 10^{4} }
\end{align*}
応用:なぜΠV=nRTなのか
ここからは入試レベルを超えるので、
興味がない場合は読み飛ばしてしまって構いません。
ファントホッフの法則は、
なぜ理想気体の状態方程式と一致するのでしょうか。
以下ではかなりラフに、
これについて考えてみます。
実は高校化学で「浸透圧」というとき、
厳密には「希薄溶液の浸透圧」を指しています。
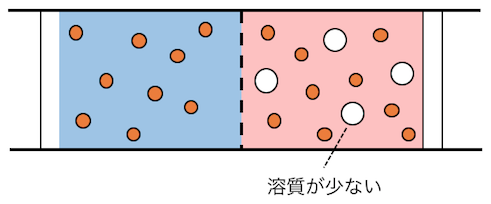
広い溶媒の空間に浮かんだ溶質の分子は、
あたかも気体のように広い空間に広がります。
その結果、浸透圧は、
真空中に溶質だけが気体で存在する場合の、
圧力に等しくなるのです。
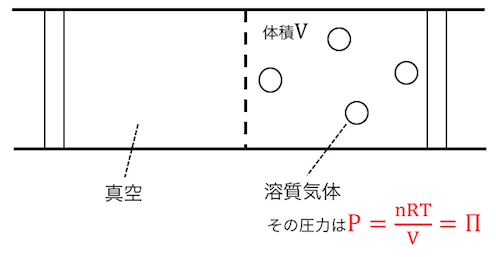
この圧力をどうにかするためには、
溶液側を力で押さえてあげる必要があります。
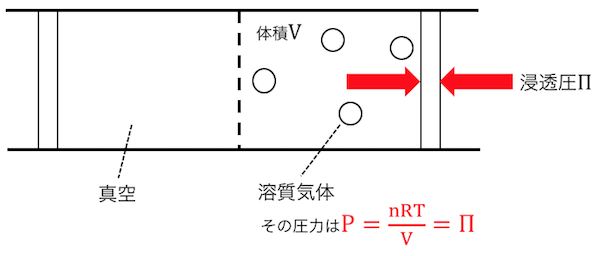
押さえないとするなら、
どうにかこの圧力を減らすために、
左から溶媒が流れ込んで体積を大きくしようとします。
これが「浸透」ですね。
以上、かなりラフな議論でしたが、
式のイメージが伝わればいいなと思います。
まとめ
今回は浸透圧の解説でした。
浸透圧は定義がわかりにくいですが、
先ほどの絵で理解しておけば大丈夫ですね。

浸透圧の問題自体は難しくないので、
きちんと練習して計算ミスをしないようにしておきましょう。














コメントを書く