高校化学の反応速度論の解説です。
あなたは反応速度式の意味や使い方、
活性化エネルギーなどの意味を正しく理解していますか?
高校ではなかなか時間をかけて教えられず、
意外と頭に残っていない受験生が多いです。
しかし反応速度論は、
定義の本質的な意味を理解した上で順に見れば、
全く難しい分野ではありません。
ここでは反応速度論の本質的なテクニックをお伝えします。
ここの内容を理解することで、
反応速度の考え方を網羅的に理解することができ、
もう反応速度の問題で手が止まることはなくなります。
それでは順番に見ていきましょう。
目次
反応速度とは
黒煙を燃やす反応と、鉄が錆びる反応を見てみましょう。
\mathrm{C + O_{2}} &→ \mathrm{CO_{2}} \\
\mathrm{4Fe + 3O_{2}} &→ \mathrm{2Fe_{2}O_{3}}
\end{align*}
どちらも見た目は同じです。
しかし黒煙は瞬く間に燃えきってしまう一方、
鉄はゆっくり時間をかけて反応していきます。
このように、
化学反応には速度の違いがあるのです。
この速度の違いがどのように生まれるのか、
順番に見ていきましょう。
反応速度を決める要因
反応速度を決める要因を探るために、
まずは化学反応の仕組みを見てみましょう。
化学反応の仕組み
化学反応は分子同士が衝突することで始まります。
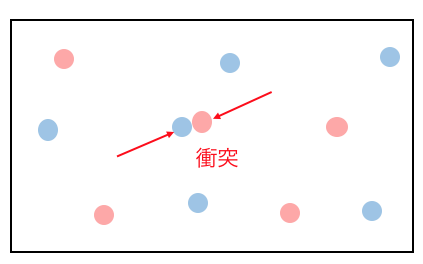
でもただぶつかるだけでは反応が起きません。
ある程度勢いよくぶつからないといけないのです。
もう少し具体的言えば、
衝突のエネルギーがある一定の値を超えると、
初めて反応が起こります。
この「ここを超えると反応するよ」
というエネルギーのことを「活性化エネルギー」といいます。
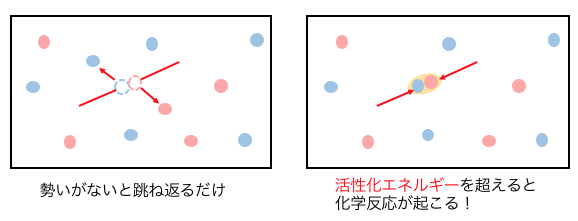
以上のことから、
①衝突回数
②分子の運動エネルギー
③活性化エネルギー
となります。
以下で詳しく説明していきますね。
①衝突回数
化学反応は分子同士の衝突で始まるんだから、
衝突の回数が多いほど反応が進みやすいです。
じゃあどういうときに衝突回数が多いかというと、
物質の濃度が高い場合です。
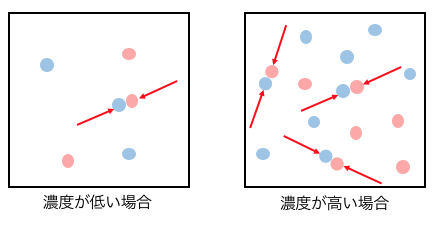
田舎ではなかなか人に会わないけど、
渋谷のスクランブル交差点では嫌でも人にぶつかるイメージです。
濃度が2倍になれば衝突する確率も2倍になりそうです。
結局のところ、
反応速度は物質の濃度に比例します。
例えば、
\[\mathrm{ 2H_{2}O_{2} → 2H_{2}O + O_{2}}\]
という反応であれば、
\[
\mathrm{ v = k[H_{2}O_{2}] }
\]
のように濃度に比例した式でかけます。
(kを「反応速度定数」と呼びます。)
②分子の運動エネルギー
化学反応が起こるためには、
勢いよくぶつかる必要があります。
つまり分子の運動エネルギーが大きいほど、
反応が起こりやすいのです。
分子の運動エネルギーは、
温度を高くするほど大きくなるのでした。
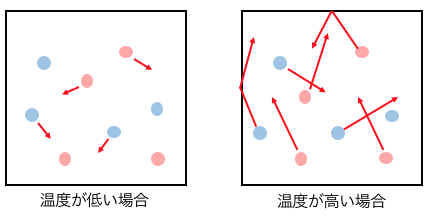
ちなみに温度を10Kあげると
反応速度は2〜3倍になります。
③活性化エネルギー
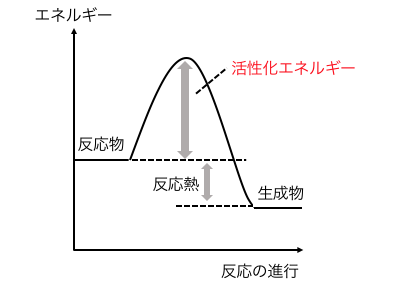
活性化エネルギーは、
衝突したときに反応が起こるのに必要なエネルギーでした。
活性化エネルギーが大きい場合は、
より大きな運動エネルギーが必要ですから、
反応の速度が遅くなります。
逆も同様ですね。
活性化エネルギーを低くするのが「触媒」です。
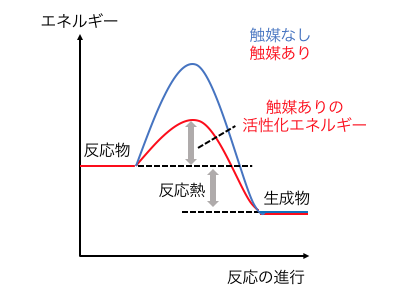
反応速度まとめ
以上をまとめると、
反応速度は以下のようになります。
\mathrm{ aA + bB → cC } \]
のCの生成速度は、
\[
\mathrm{v = k[A]^{a}[B]^{b}}
\]
であり、反応速度係数kは触媒と温度に依存します。
「なんで[A]と[B]が掛け算?」
「なんでa乗とかb乗とかになるの?」
という場合は以下のアンモニアの式を例に考えましょう。
\mathrm{ N_{2} + 3H_{2} } &→ \mathrm{ 2NH_{2} } \\
\mathrm{ N_{2} + H_{2} + H_{2} + H_{2} } &→ \mathrm{ 2NH_{2} }
\end{align*}
この反応の反応速度は、
窒素の濃度にも、1つ目の水素の濃度にも、
2つ目の水素の濃度にも、3つ目の水素の濃度にも、
それぞれ比例するはずです。
よって、
\begin{align*}
\mathrm{ v } &= \mathrm{ k[N_{2}][H_{2}][H_{2}][H_{2}] } \\
&= \mathrm{ k[N_{2}][H_{2}]^{3} }
\end{align*}
このようになります。
窒素が2倍になれば速度が2倍、
水素が2倍になれば速度が8倍になるということですね。
反応速度を実験的に求める場合
ここで少し実践的な話に移ります。
ここまでは反応速度の理論的な話でしたが、
反応速度を実験によって測定することもあります。
反応速度を測定する目的は、
反応速度定数kを求めること。
これに注意して読んでみてください。
平均の速さ
このような反応を考えてみます。
この反応の進み方は以下のようになったとします。
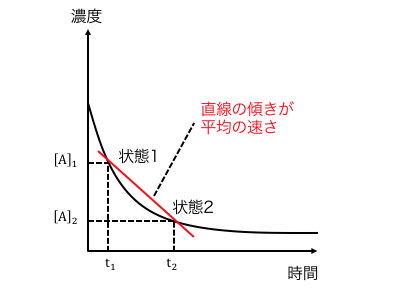
このとき、状態1から状態2へ移るときの、
平均の速さ\(\mathrm{\bar{v}}\)が求まります。
\[
\mathrm{ \bar{v} = \left | \frac{[A]_{2}-[A]_{1}}{t_{2}-t_{1}} \right |}
\]
瞬間の速さの近似
平均の速さと反応速度定数kを結びつけます。
先ほどのグラフの直線を下に下げていくと、
だいたい状態1と状態2の中間で接しますね。
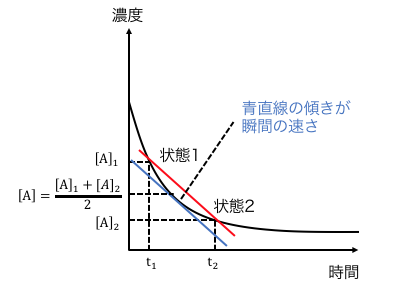
以上から、
状態1と状態2の平均の速さは、
その中間の瞬間の速さと一致すると近似します。
これを式で表すと以下。
\[
\mathrm{ [\bar{v}] } = \mathrm{k[\bar{A}]}
\]
\(\mathrm{[\bar{v}]}\)も\(\mathrm{[\bar{A}]}\)も実験で測定できますから、
反応速度定数kを求めることができますね。
おそらくこれだけでは少しイメージが湧かないと思うので、
実際の問題で考えてみましょう。
例題:過酸化水素の分解
(1)平均の反応速度[\(\mathrm{\bar{v}}\)]は何mol/(L・s)か。
(2)この間の平均濃度を[\(\mathrm{\overline{H_{2}O_{2}}}\)]とすると、反応速度式は\(\mathrm{[\bar{v}]=k[\overline{H_{2}O_{2}}]}\)と表せる。反応速度定数kはいくつか。
(1)平均の速度は定義通り、
\[\mathrm{ \bar{v} = \frac{0.40-0.25}{(8-4)\times 60} =6.25\times 10^{-4}}\]
(2)2つの状態の平均の濃度は、
\[\mathrm{ [\bar{H_{2}O_{2}}] = \frac{0.40+0.25}{2} = 0.325}
\]先ほど説明した近似式\(\mathrm{[\bar{v}]=k[\overline{H_{2}O_{2}}]}\)が与えられていますね。これを使えば、
\begin{align*}
\mathrm{ [\bar{v}] } &= \mathrm{k[\overline{H_{2}O_{2}}]} \\
\mathrm{ 6.25\times 10^{-4} } &= \mathrm{k\times 0.325} \\
\mathrm{k} &≒ \mathrm{ 1.9\times 10^{-3} }
\end{align*}
参考:瞬間の速度
ここからは少しだけ高校範囲を超えますが、
瞬間の速度をしっかりと考えてみます。
難関大ではたまに出題されるので、
軽く目を通しておくといいでしょう。
先ほどの平均の速度の式で、
\(\mathrm{ \Delta t = t_{2}-t_{1} }\)、\(\mathrm{ \Delta [A] = [A]_{2}-[A]_{1} }\)とします。
さらにAは減少していることに注意すると、
\[
\mathrm{ \bar{v} = -\frac{\Delta [A]}{\Delta t} }
\]
となります。
「瞬間」の速度というくらいだから、
\(\mathrm{ \Delta t}\)としてしまいましょう。
そうすると結局これは微分の式になります。
\[
\mathrm{ v = -\frac{d[A]}{dt} }
\]
もうこの式は瞬間の速度を表していることに注意してください。
つまり\(\mathrm{v=k[A]}\)を使って、
\[
\mathrm{ -\frac{d[A]}{dt} = k[A]}
\]
このように濃度[A]に関する方程式になりました。
しかしよく見るとこれはy’=yのような形で
微分方程式を習っていない高校生では解けません。
そこで答えだけ書くとこのようになります。
\[
\mathrm{ [A] = A_{0} e^{-kt}}
\]
このように指数関数的に変化するのです。
まとめ
今回は反応速度の解説でした。
反応速度論は大学の化学でも主要な分野で、
高校生にとっては少し難し分野です。
この記事を何度も読み返して、
きっちりと理解しておきましょう。













コメントを書く