「固体の溶解度の計算問題が解けない」
「溶解度は問題のパターンが多すぎる」
「何やら公式がたくさんあるなあ」
あなたもこのように感じたことはありませんか?
受験生の指導をしていても、
毎年のように溶解度の質問が飛んで来ます。
固体の溶解度の計算問題が解けないのは、
「公式」の無駄な暗記に気をとられてしまって、
溶解度の本質的な考え方を理解していないからです。
ここでは溶解度の本質的な考え方を、
実際の問題を使いながら解説しますね。
ここの内容を最後まで理解することで、
溶解度のさまざまな問題がすべて同じものに見え、
「公式なんて覚える必要ないじゃん!」と思えるようになります。
ぜひ最後まで読み飛ばさずに読むことで、
溶解度を完璧にマスターしちゃってください。
固体の溶解度と溶解度曲線
まずは固体の溶解度の意味を理解していきましょう。
固体の溶解度の計算ができない場合は、
溶解度の意味を分かっていないことが多いです。
では説明していきます。
固体の溶解度とは
「固体の溶解度」とは、
溶媒に溶かすことができる限界の量です。
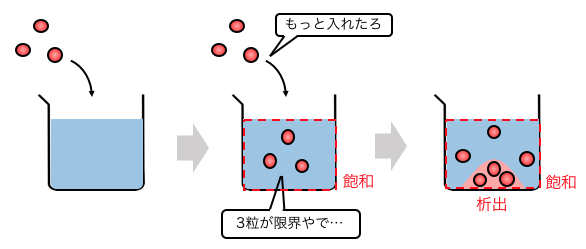
水に塩をいれていくと、
最初は入れれば入れるほど溶けますが、
大量に入れていくと溶けきらなくなりますね。
このような「限界まで溶けている状態」を「飽和」といいます。
通常固体の溶解度は、
溶媒100gに対して溶質が何g溶けるか
によって定義されます。
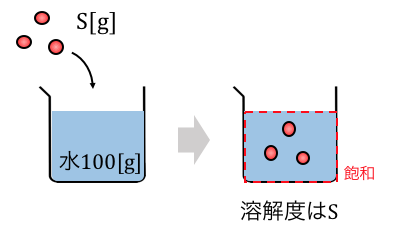
まずはこの定義をよく理解しておきましょう。
水100gを用意して、
そこに塩を少しずつ入れていったときに、
溶け残りが生じるまでに必要な塩の量が溶解度です。
頭にイメージが浮かぶと覚えやすいと思います。
溶解度曲線
水に塩や砂糖を溶かすとき、
熱いお湯の方がたくさん溶けますよね。
このように、
温度が上がるほど溶解度も上がります。
温度と溶解度の関係をグラフにしたものが、
「溶解度曲線」です。
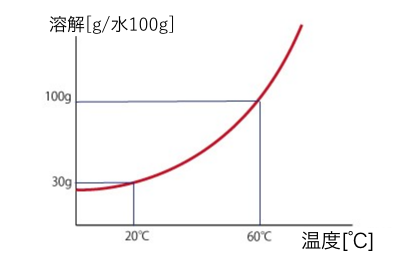
例えばこのグラフは、
KNO3は10℃の水100gに20g溶ける
と読みます。
固体の溶解度の計算問題
さて、それでは溶解度を使った計算問題を見ていきましょう。
固体の溶解度の問題が出ると生徒から、
「この問題はどの公式を使いますか?」
というような質問が必ず来ます。
でもそもそも溶解度の計算問題で、
公式を使うという意識自体が間違っています。
これがどういうことかを、
以下で説明していきましょう。
立式の考え方
水に塩を溶かすことを考えてみてください。
もし水100gに塩が40g溶けるとしたら、
水200gにはどれだけの塩が溶けるでしょうか。
「そんなの当然80g!」と思いますよね。
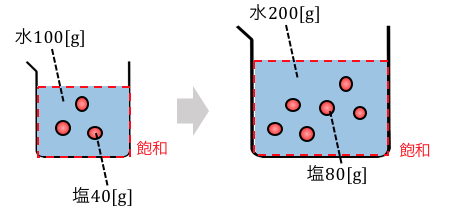
これが何を指しているかというと、
飽和状態であれば水の量に関係なく濃度が同じなのです。
溶解度の問題ではこのように、
飽和状態の濃度が同じことに注目して式を立てるのです。
例えば「溶質」と「溶媒」の量に注目すれば、
以下のような立式になります。
\mathrm{ \frac{溶質[g]}{溶媒[g]}=\frac{溶解度S}{水100[g]} }
\]
この式は、
飽和状態なら濃度が同じだよ
と読むことができますね。
同じように「溶質」と「溶液」に注目すれば、
以下のような立式になります。
\mathrm{ \frac{溶質[g]}{溶液[g]}=\frac{S}{100+S} }
\]
この式も同じように、
飽和状態なら濃度が同じだよ
と読むことができます。
溶解度の問題で立式するときは、
ただ飽和状態の濃度を比べているだけなのです。
こうして考えれば公式という感覚はなくなりますね。
それでは具体的な問題で考えてみましょう。
例題:ホウ酸水溶液
(1)60℃の飽和ホウ酸水溶液100gを作るのに必要なホウ酸は何gか。
(2)(1)を20℃に冷却したときに、析出するホウ酸は何gか
まずは現象を確認してみましょう。
求めたいホウ酸の質量をxとします。
飽和状態で溶液が100gということは、
以下のような状態ですね。
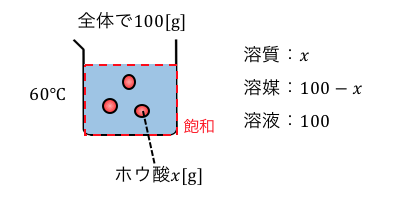
これが飽和ということなので、
溶解度を使って濃度を比較しましょう。
溶質x、溶媒100-x、溶液100だから、
溶質と溶液を使うと式が立てやすそうです。
\begin{align*}
\mathrm{ \frac{溶質[g]}{溶液[g]} } &= \mathrm{ \frac{S}{100+S} } \\
\mathrm{ \frac{x}{100} } &= \mathrm{ \frac{15}{100+15} } \\
\mathrm{ x } &≒ \mathrm{ 13[g] }
\end{align*}
現象が観察できれば全く難しくないですね。
\begin{align*}
\mathrm{ \frac{溶質[g]}{溶媒[g]} } &= \mathrm{ \frac{S}{100} } \\
\mathrm{ \frac{x}{100-x} } &= \mathrm{ \frac{15}{100} } \\
\mathrm{ x } &≒ \mathrm{ 13[g] }
\end{align*}さらに言えば、溶媒と溶液で考えても解けます。「溶液全体に対する水の濃度」を比べているイメージです。
\begin{align*}
\mathrm{ \frac{溶媒[g]}{溶液[g]} } &= \mathrm{ \frac{100}{100+S} } \\
\mathrm{ \frac{100-x}{100} } &= \mathrm{ \frac{100}{100+15} } \\
\mathrm{ x } &≒ \mathrm{ 13[g] }
\end{align*}これらは公式ではなく、単に濃度を比べているだけなのです。
それでは次に(2)を見ていきます。
こちらもまずは現象をよく見るのが大切です。
析出したホウ酸の質量をyとします。
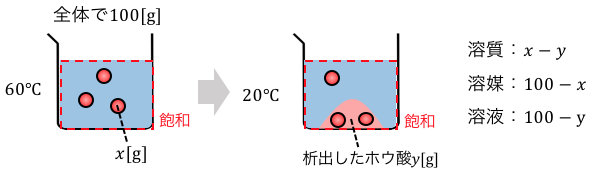
xは60℃のホウ酸水溶液100gに溶けている、
ホウ酸の質量でしたね。
文字が2つになって一瞬複雑に見えますが、
きっちり指差し確認していけば意味がわかりますね。
それでは式を立てていきましょう。
今、20℃の状態でホウ酸が析出しているということは、
飽和状態になっているということです。
よって20℃の溶解度と、濃度を比べられますね。
\begin{align*}
\mathrm{ \frac{溶質[g]}{溶媒[g]} } &= \mathrm{ \frac{S}{100} } \\
\mathrm{ \frac{x-y}{100-x} } &= \mathrm{ \frac{15}{100} } \\
\mathrm{ \frac{13.0-y}{100-13.0} } &= \mathrm{ \frac{15}{100} } \\
\mathrm{ y } &≒ \mathrm{ 8.7[g] }
\end{align*}
(1)(2)と問題の中身は違いますが、
本質は全く一緒ですね。
溶解度の問題の注意点
このように溶解度の計算問題は、
いつも「現象を捉えて、濃度(比)を考える」だけです。
だからその場その場で、
状況にあった解法を選べるのですね。
しかしそのせいで、
参考書の模範解答のやっていることが、
理解できなくなることがよくあります。
例えば先ほどの(2)を考えます。
これは先ほど普通にやれば解けました。
しかし以下のような2つの状況を比べることもできます。
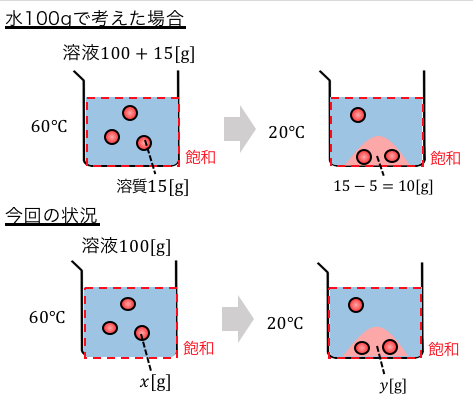
すると、
60℃の溶液115gを20℃に冷却すると10g析出する
60℃の溶液100gを20℃に冷却するとyg析出する
という2つの状況があることがわかります。
「最初に用意した溶液」に対する「析出量」で、
仮の濃度のようなものを考えれば以下のように計算できます。
\begin{align*}
\mathrm{ \frac{析出量[g]}{60℃の溶液[g]} } &= \mathrm{ \frac{S_{60℃}-S_{20℃}}{100+S_{60℃}} } \\
\mathrm{ \frac{y}{100} } &= \mathrm{ \frac{15-5}{100+15} } \\
\mathrm{ y } &≒ \mathrm{ 8.7[g] }
\end{align*}
なにも知らない人がこれを見れば、
「わー、析出量の公式もあるのかー!」
と思ってしまいますよね。
しかし実際はそんなことはなく、
飽和ではいつも濃度が一定になることを使っているだけなのです。
こんな解法に出会っても慌てずに、
どこの濃度を比べているのかを順番に確認してみましょう。
まとめ
今回は固体の溶解度の解説でした。
固体の溶解度とは、
溶媒100gの中にどれだけ溶けることができるか
の値でしたね。
これをしっかりと理解していれば、
例えば以下のような「公式」も覚えなくても良いのでした。
\mathrm{ \frac{溶質[g]}{溶媒[g]} } &= \mathrm{ \frac{S}{100} } \\
\mathrm{ \frac{溶質[g]}{溶液[g]} } &= \mathrm{ \frac{S}{100+S} }
\end{align*}
これを理解せずに暗記してしまうと、
「析出量の公式」やらなんやらまで覚えることになってしまいます。
きっちりと現象を理解して、
その場で立式できるようにしていきましょう。














コメントを書く