「アルキメデスの原理の意味がわからない」
「水圧や浮力の求め方が理解できない」
力学の中でも浮力は盲点になりやすく、
意外と勉強が追いつかない場合も多いですよね。
浮力の分野では、
今までなかった「圧力」が関わるため、
なんとなく難しく感じがちです。
この記事では画像を使いながら浮力を解説していきますね。
この記事を読めば、
水圧や浮力の求め方がうまくイメージでき、
浮力関連の問題は簡単に解けるようになります。
受験生がつまづきやすい、
アルキメデスの原理も解説していきます。
ぜひ最後まで読んでいってください。
浮力とは?アルキメデスの原理を解説!
プールの中では体が軽くなり、
水の上に浮くことができます。
水中では「浮力」という力が生じるからです。
浮力はその名の通り、
水中(流体中)にいる物体にかかる、
浮き上がる力ですね。

今回は浮力の大きさを求めていくのですが、
そのためには「水圧」を考えなければいけません。
これまでに出てきていない、
「圧力」が関係してくる話で、
少しややこしいですが一緒に頑張っていきましょう。
浮力の大きさの導出
水圧の大きさの導出
「水圧」とはその名の通り、
水による圧力のことです。
水は一粒一粒の水分子からなっており、
すべての水分子に重力がかかっています。
水深が深いところへ行くほど、
上に水分子が積み重なってくるため、
どんどん重力の影響が大きくなります。
このイメージ通り、
水圧は水深が深いほど大きくなるのです。
それでは実際に水圧を求めてみましょう。
水槽の中から、図のように
断面積S、高さhの円柱に注目します。
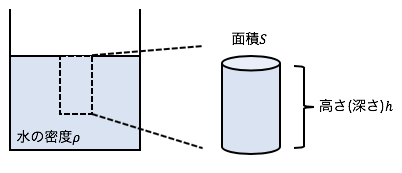
当然、この円柱には重力が働きます。
円柱の質量は水の密度\rhoを用いて、
\rho Shと表せます。
これは一見わかりにくいですが、
Shが円柱の体積V=Shを表しており、
密度×体積=質量によって求めています。
よって円柱にかかる重力は\rho Shgです。
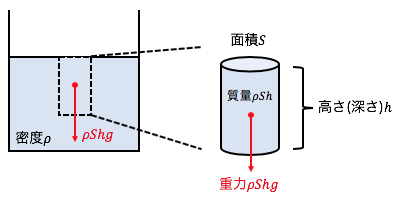
もし円柱に重力だけが働けば、
円柱部分だけが沈んでいってしまいますが、
もちろんそんなことはありえません。
円柱の下から水圧がかかることで、
円柱が支えられているのです。
水圧をpとして、力=圧力×面積に注意すると、
水圧による力はpSとなります。
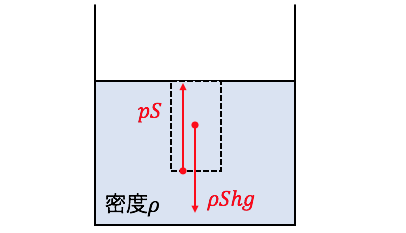
あとは力の釣り合いを考えれば、
以下のように水圧pが求まります。
\begin{align*} pS &= \rho Shg \\ p &= \rho hg \end{align*}
このようにして水圧が求まりました。
水圧は液体の密度と深さだけで決まるのですね。
\begin{align*} pS &= p_{大気圧}S + \rho Shg \\ p &= p_{大気圧} + \rho hg \end{align*}
浮力の大きさの導出
水圧が求まったところで、
さっそく浮力を求めていきましょう。
物体を沈めると四方八方から水圧がかかり、
それによって四方八方から力を受けます。
この力を全部合わせた結果が浮力です。
それでは断面積S、高さhの物体を水に沈め、
その浮力を考えてみましょう。
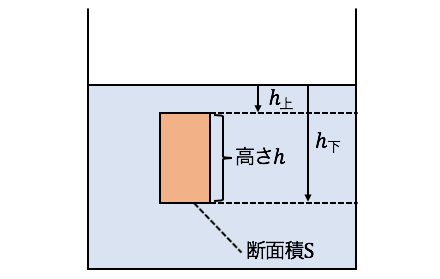
沈めた物体の上面の水深をh_{上}、
下面の水深をh_{下}とします。
先ほどは円柱状の水を考えていましたが、
今回は物体を沈めていることに注意しましょう。
先ほど求めた通り、
水深によって水圧の大きさが変わりました。
つまり同じ深さの水圧は同じということです。
これによって、
物体の側面から働く圧力は、
左右で釣り合って消えてしまうことがわかります。
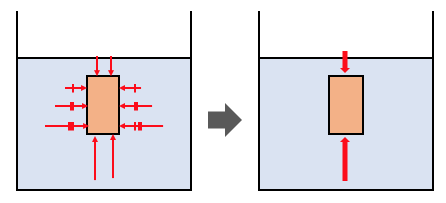
残るのは上面と下面に働く圧力のみです。
上下に働く力は以下の通り。
\begin{align*} F_{上} &= p_{上}S = p_{大気圧}S + \rho Sh_{上}g \\ F_{下} &= p_{下}S = p_{大気圧}S + \rho Sh_{下}g \end{align*}
浮力はこれらの力の合計だったから、
上向きに働く浮力F_{浮力}は以下のように求まります。
\begin{align*} F_{浮力} &= F_{下}-F_{上} \\ &= (p_{大気圧}S + \rho Sh_{下}g) – (p_{大気圧}S + \rho Sh_{上}g) \\ &= (h_{下}-h_{上})\rho Sg \\ &= \rho Shg \end{align*}
このようにして浮力が求まりました。
物体の体積をV=Shとするなら、
F_{浮力} = \rho Shg = \rho Vg
となります。
アルキメデスの原理
先ほどは円柱状の物体への浮力を考えましたが、
実は一般にどんな形の物体でも同じように表せます。
このように一般の物体に対して、
浮力の大きさをした原理を「アルキメデスの原理」といいます。
厳密な証明は大学レベルになってしまうので、
この記事の上では省略しますが、
根本的な考え方は円柱とまったく同じです。
アルキメデスの原理では、
先ほど導出した浮力の式を、
以下のように解釈します。
水中の物体は、その物体が押しのけた水の重力に等しい浮力を受ける。
少しわかりにくいと思うので、
少し丁寧に説明しますね。
まずは先ほどの式を思い出します。
F_{浮力} = \rho Vg
この式の中の\rho Vは、
(水の密度)×(体積)を表しているので、
結果的に水の質量を表しています。
すると\rho Vgは水の重力を表しているわけです。
これを図で確認します。
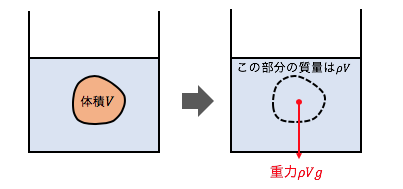
体積Vは物体の体積をですから、
\rho Vは物体の体積分の水です。
これを「物体が押しのけた水」と呼んでいるのです。
よって浮力は、
物体が押しのけた水の重力に等しい
と言えますね。
このように日本語で理解しておくと、
式を丸暗記しているより思い出しやすいので、
ぜひこちらで覚えておきましょう。
物体の浮き沈み
さて、ここまで浮力を見てきました。
でもこんな疑問が湧く人もいそうです。
例えば鉄球を水に沈めれば、
すぐに沈んでいってしまいそうですが、
発泡スチロールを水に沈めようとしても、
すぐに水面に浮いてきてしまいます。
でも鉄球も発泡スチロールも、
体積が同じなら浮力は同じです。
この違いはなんなの?
この疑問は冷静に力の図示をすれば、
すぐに解決できます。
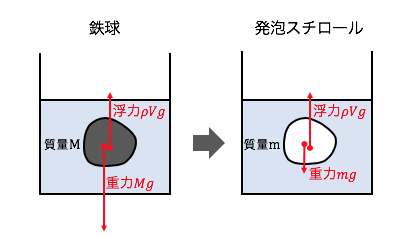
水中にいれた物体には、
浮力だけでなく重力など他の力もかかります。
鉄球は重力が大きいから沈んでいき、
発泡スチロールは重力が小さく、
浮力の影響が大きくなりやすいから浮き上がるのです。
言われてみれば当然ですね。
ちなみに物体が沈む間に、
浮力と重力が釣り合う場合は、
物体が水中で止まるということになります。
浮力だって力の一種なので、
浮力の大きささえ求めることができれば、
あとは今まで通り運動方程式で考えられるのです。
まとめ
今回は浮力の解説でした。
浮力は「圧力・水圧」が関わる分、
少し複雑に感じましたね。
しかし一旦力の求め方を理解して、
アルキメデスの原理を理解してしまえば、
あとはただの力の一種として扱えます。
きっちり理解しておきましょう。













コメントを書く