高校物理の円運動では、
速度の公式、加速度の公式などなど、
色々と覚える公式が出てきます。
しかし円運動をきっちり理解できている受験生は少ないです。
円運動が難しく感じるのは、
円運動が発生する仕組みを理解していなく、
公式の意味を本質的に理解していないからです。
ここでは円運動をわかりやすく解説していきますね。
この記事を最後まで読むことで、
円運動の公式が本質的に理解できるだけでなく、
円運動の問題の解法にも迷わなくなります。
力学の解法が思いつかないのは、
このような基礎的な部分の問題なのです。
ぜひ最後まで読んでみてください。
円運動とは?
「円運動」とはその名の通り、
物体が円形にぐるぐる回る運動です。
円運動がどのように起こるのか、
以下のようにイメージしてみましょう。
まず単純に、
ボールが等速直線運動をしているとします。

このボールを途中で引っ張ったとしましょう。
今回は上向きに引っ張ってみます。
すると当然、上に少し曲がりますね。

さらにボールが曲がった後も、
進行方向に対して垂直に引っ張り続けると、
以下のような運動になります。

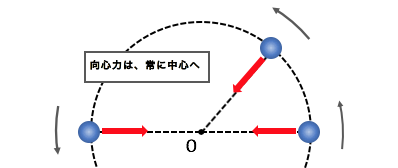
以上のように、
進行方向に垂直な力を加えることで、
円運動が発生します。
円運動の原因となるこの力を、
「向心力」と呼びます。
なんとなく円運動のイメージがついたでしょうか。
円運動の速度・加速度
円運動のイメージがついたところで、
具体的な取り扱い方を考えていきます。
既に勉強した通り、
何か運動を考えたかったら、
運動方程式を考えるのが普通です。
しかし今回は、
今まで通り考えることはできません。
まずはその理由から見ていきます。
円運動は「極座標」で考える
今まで、運動方程式を考えるとき、
常にxy座標で考えてきました。
例えば斜方投射などの問題でも、
x軸方向とy軸方向の力に注目して、
それぞれで運動方程式を立てましたね。
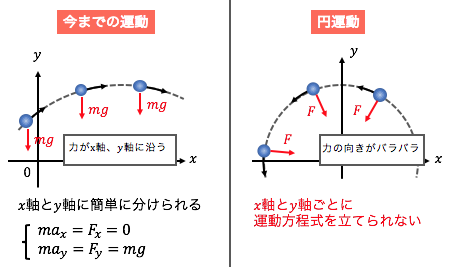
しかし結論から言えば、
円運動をxy座標で考えるのは難しいです。
なぜなら今までの力は、
原則x軸やy軸に沿った方向の力でしたが、
円運動を引き起こす向心力は向きが変わるからです。
では円運動をどのように扱うのか。
これも結論から言ってしまえば、
xy座標ではなく、中心角θを変数にして考えます。
つまり、「極座標」を用いるのです。
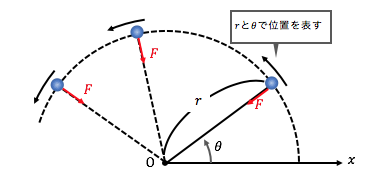
極座標は丸っこい図形の扱いが得意で、
いかにも円運動を考えやすそうですね。
力や速度、加速度を考えるとき、
xy座標では、「x軸方向」と「y軸方向」
に分けて考えてきました。
しかし極座標では、
「接線方向」と「中心方向」に分けて
考えます。
接線方向はθが変化する方向に、
中心方向はrが変化する方向に対応しています。
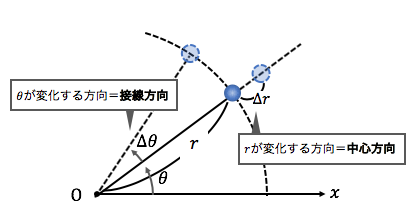
まさに向心力を扱うにはちょうどいいですね。
円運動の速度
それでは円運動の速度を考えます。
まず円運動では半径が一定ですから、
中心方向の速度は0です。
次に接線方向の速度です。
以下の図を見てください。
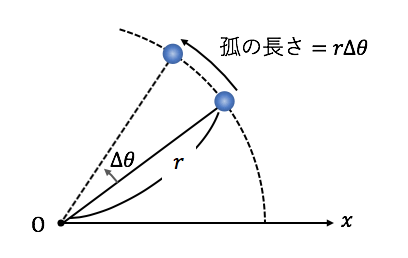
時間\(\Delta t\)の間に中心角が\(\Delta\theta\)進んだ場合、
接線方向には\(r\Delta\theta\)進んでいます。
これは「ラジアン」の定義からすぐにわかります。
よってxy座標の速度の定義と同じように考えれば以下の通りです。
\begin{align*}
v_{接} &= \lim_{\Delta t \to 0}\frac{r\Delta\theta}{\Delta t} = r\frac{d\theta}{dt} = r\omega\\
&(ただし\omega=\frac{d\theta}{dt})
\end{align*}
ωは時間に対する角度の変化具合であり、
「角速度」と呼びます。
以上をまとめれば、
円運動の速度は以下のようになります。
中心方向 \(v_{中}=0 \)
接線方向 \(v_{接}=r\omega \)
(ただし\(\omega=\frac{d\theta}{dt}\)は角速度)
円運動の加速度
次に円運動の加速度を考えます。
加速度はの導出は少し難しいので、
まずは結論を書いてしまいます。
導出に興味がなければここだけ押さえてしまいましょう。
中心方向 \(a_{中}=r\omega^2=\frac{v_{接}^2}{r} \)
接線方向 \(a_{接}=\frac{dv_{接}}{dt} \)
まずは簡単な接線方向から。
\(\Delta t\)の間に物体の位置が微妙に変化して、
同時に速度が\(\Delta v_{接}\)変化したとします。
物体は円運動をしていると言っても、
ごく短い時間では接線方向に直線運動している、
とみなすことができます。
よって接線方向の加速度は、
xy座標のときと同じように求まります。
\[ a_{接} = \lim_{\Delta t \to 0}\frac{\Delta v_{接}}{\Delta t}=\frac{dv_{接}}{dt} \]
次に中心方向です。
先ほどと同じように、
\(\Delta t\)の間の変化を図に表します。
このときの中心方向の変化に注目してみましょう。
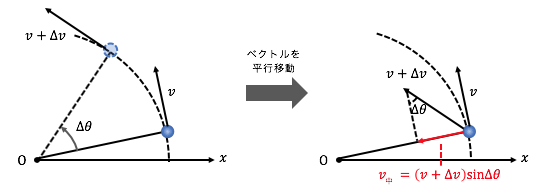
このように中心方向に速度が変化しています。
この速度変化が中心方向の加速度です。
あとは今まで通り\(\lim_{\Delta t \to 0}\frac{\Delta v_{中}}{\Delta t}\)を考えますが、
今までとは違って近似が現れます。
\(\Delta\theta\)や\(\Delta v_{中}\)は非常に小さいので、
・\(sin\Delta\theta≒\Delta\theta\)
・\(\Delta v\Delta\theta≒0\)(二次の微小量)
が成り立つことを使うと、
\begin{align*}
a_{接} &= \lim_{\Delta t \to 0}\frac{\Delta v_{中}}{\Delta t} \\
&= \lim_{\Delta t \to 0}\frac{(v_{接}+\Delta v_{接})sin\Delta\theta}{\Delta t} \\
&≒ \lim_{\Delta t \to 0}\frac{(v_{接}+\Delta v_{接})\Delta\theta}{\Delta t} \\
&≒ \lim_{\Delta t \to 0}\frac{v_{接}\Delta\theta}{\Delta t} \\
&= v_{接}\frac{d\theta}{dt}
\end{align*}
角速度や接線方向の速度を思い出せば、
\[ a_{中} = v_{接}\frac{d\theta}{dt} = v_{接}\omega = r\omega^2 \]
以上で接線方向の加速度も求まりました。
結果をもう一度まとめておきます。
中心方向 \(a_{中}=r\omega^2=\frac{v_{接}^2}{r} \)
接線方向 \(a_{接}=\frac{dv_{接}}{dt} \)
円運動の運動方程式
円運動の加速度が求まったので、
\(r\)と\(\theta\)を変数に取る極座標に対応した、
円運動の運動方程式を使えるようになりました。
中心方向 \(mr\omega^2=m\frac{v_{接}^2}{r}=F_{中} \)
接線方向 \(m\frac{dv_{接}}{dt}=F_{接} \)
これで円運動も運動方程式で解くことができます。
ちなみに実際の問題では、
接線方向の力\(F_{接}=0\)の場合も多いです。
このとき接線方向の運動方程式から、
接線方向の速度\{v_{接}\}は一定になるため、
「等速円運動」になります。
雑談:円運動の加速度について
中心方向に加速度が生じているのに、
中心方向の速度が0、というのは不思議ではありませんか?
これは一番最初に説明した、
円運動の発生の仕方を思い出せば解決できます。

物体がもともと直線運動をしていて、
そこに向心力を加えることで、
円運動を発生させたと考えます。
すると接線方向の速度とはつまり、
もともとの直線運動の速度ですから、
加速度は今まで通り表せるわけです。
\(a_{接}=\frac{dv_{接}}{dt}\)
そして直線運動に向心力を加えることで、
円運動が発生します。
何もしなければ直線運動する物体に、
中心方向の加速度を加えることで、
接線方向の速度の向きが変えられているのです。
つまり中心方向の加速度は、
接線方向の速度に影響を与えていることになります。
中心方向の加速度は、
半径rの円運動の軌道を保つために、
速度の向きを変えるのに使われており、
中心方向の速度には使われていないのですね。
まとめ
今回出てきた数式をまとめておきましょう。
中心方向 \(v_{中}=0 \)
接線方向 \(v_{接}=r\omega \)
(ただし\(\omega=\frac{d\theta}{dt}\)は角速度)
円運動の加速度
中心方向 \(a_{中}=r\omega^2=\frac{v_{接}^2}{r} \)
接線方向 \(a_{接}=\frac{dv_{接}}{dt} \)
円運動の運動方程式
中心方向 \(mr\omega^2=m\frac{v_{接}^2}{r}=F_{中} \)
接線方向 \(m\frac{dv_{接}}{dt}=F_{接} \)
この記事では円運動の理解を促すため、
きちんと全ての導出を行いましたが、
現実的に運動方程式は覚えておくべきです。
覚える量は大したことないので、
今すぐ覚えてしまいましょう。
では今回はここまで。














コメントを書く