「問題演習で急に束縛条件が出てきた」
「束縛条件ってなんのためにあるの?」
「難関大用の難しい概念なのかな…」
あなたもこんな風に考えたことはありませんか?
束縛条件は授業でも軽く飛ばされ、
問題演習で急に考えさせられることも多く、
苦手に思っている人も多いでしょう。
中には『特殊な難しい概念』と勘違いしている人もいます。
あなたが束縛条件を苦手に思うのは、
束縛条件が本質的にどんなものなのかを知らず、
闇雲に理解しようとしているからです。
ここでは束縛条件のみに絞って解説を行います。
この記事を読めば、
束縛条件の意味を本質的に理解でき、
さらに束縛条件が当然のものに思えるようになります。
今までモヤモヤしていた力学の疑問が、
綺麗に解消するでしょう。
ぜひ最後まで読み飛ばさずに読んでみてください。
束縛条件って何?
物体が運動をするとき、
このレールの上でしか動けない
この坂道の上でしか運動できない
と言うような「位置的な条件」がある事があります。
このような条件のことを、
「束縛条件(拘束条件)」と呼びます。
束縛条件には例えば以下のようなものがあります。
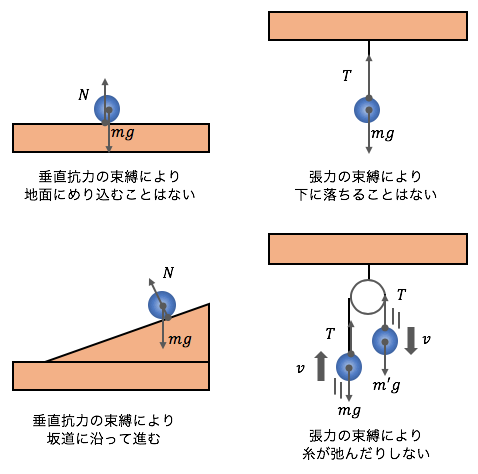
以上のように、
地面や坂道を突き抜けたりしないだとか、
糸は切れないし弛まないだとか、
そのような現実の条件を表しています。
感覚的には理解しやすいですね。
しかし束縛条件が存在する問題を解くには、
この条件を数式として書く必要があります。
次の章では、
束縛条件を数式で表現する方法、
について見ていきましょう。
束縛条件を数式で表現する
束縛条件は「位置的な条件」でした。
これを思い出しながら、
束縛条件を数式で考えてみましょう。
まずは一番単純な例で考えます。
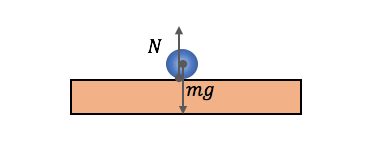
このボールは、
もし糸がなければ落ちてしまうけど、
糸が張力で束縛することで静止しています。
つまり、糸は切れたりしないから、
ボールの位置が変化しない、
というのが今回の束縛条件です。
これを素朴に式に表すと以下の通り。
\[ 位置x = (一定) \]
実はこれは別の言い方もできます。
位置\(x\)が変化しないということは、
速度が0だし、加速度も0ということです。
\[ 速度v=0、加速度a=0 \]
よって今回の束縛条件をまとめると以下の通り。
\[ 位置x=(一定)、速度v=0、加速度a=0 \]
このようにして、
束縛条件を数式で表わせました。
あとは運動方程式と連立すれば、
未知数を全て求める事ができます。
\begin{align*}
\begin{cases}
ma&=mg-T \\
a&=0
\end{cases} \\
よってa=0、T=mg
\end{align*}
束縛条件はこのように、
問題の条件によって個別に考えます。
「個別に考えるなんて面倒…」
と感じるかもしれませんが、
実は束縛条件を使う問題はある程度決まっています。
今回の記事では、束縛条件を使う頻出問題の中から、
①滑車の問題
②動く三角台の問題
の束縛条件を解説していきたいと思います。
①滑車の問題
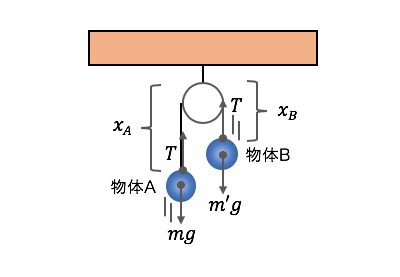
定滑車の問題を考えてみましょう。
図の物体Aと物体Bはどんな位置の条件があるでしょうか。
この問題では、
定滑車の糸が切れないし弛まない
という条件があります。
糸の長さを\(l\)とすれば、
この条件は以下の数式で表わせます。
\[ x_{A} + x_{B} = l(一定) \]
これを、先ほどと同じように、
速度や加速度でも考えると以下のようになります。
\[ v_{A} = v_{B}、a_{A} = a_{B} \]
以上をまとめると以下の通り。
\begin{align*}
x_{A} &+ x_{B} = l(一定) \\
v_{A} &= v_{B}、a_{A} = a_{B}
\end{align*}
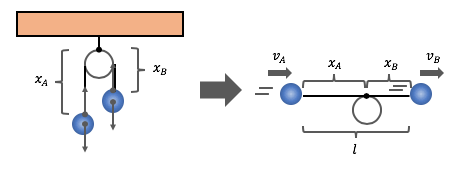
②動く三角台の問題
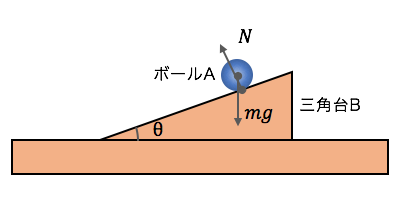
次は少しややこしい問題です。
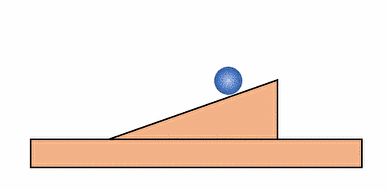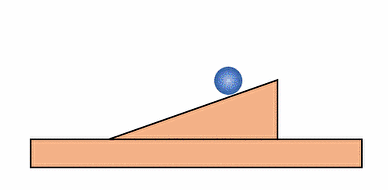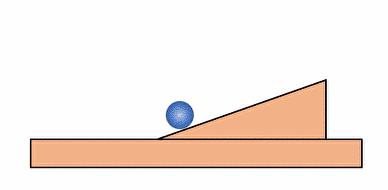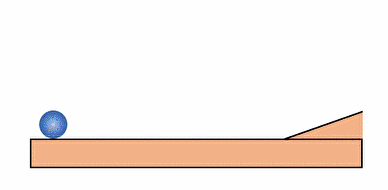
三角形の台Bが摩擦のない地面に置かれ、
その上をボールAが転がっていく、
という問題です。
ボールAが転がるときに、
三角台Bは反対側に押されて、
お互いに逆向きに移動しています。
そしてこの運動の中でも、
ボールAは坂道から離れる事はない、
これが今回の束縛条件です。
それでは束縛条件を数式にします。
ボールAの水平、鉛直の移動距離を\(x_{A}\)、\(y_{A}\)、
台Bの水平の移動距離を\(x_{B}\)とします。
このときのボールAと台Bの関係は以下の通り。
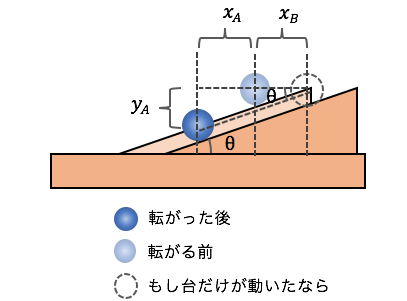
ボールAが坂道から離れないとすると、
水平方向の相対距離\(x_{A}+x_{B}\)と、
鉛直方向の相対距離\(y_{A}\)には以下の関係があります。
\[ \frac{y_{A}}{x_{A}+x_{B}} = tan\theta \]
少しイメージは湧きづらいかもですが、
横移動と縦移動をしても角度\(\theta\)の坂道にいる、
というのをこの式が表しています。
速度と加速度の関係も同様に求まります。
\begin{align*}
\frac{v_{y_{A}}}{v_{x_{A}}+v_{x_{B}}} &= tan\theta \\
\frac{a_{y_{A}}}{a_{x_{A}}+a_{x_{B}}} &= tan\theta
\end{align*}
以上に簡単な式変形をして、
まとめると以下の通り。
\begin{align*}
(x_{A}+x_{B})tan\theta &= y_{A} \\
(v_{x_{A}}+v_{x_{B}})tan\theta &= v_{y_{A}} \\
(a_{x_{A}}+a_{x_{B}})tan\theta &= a_{y_{A}}
\end{align*}
これは一度練習しておかないと、
なかなか思いつかなそうですね。
ぜひ自分でも手を動かしてみてください。
補足
以上では、
①滑車の問題
②動く三角台の問題
を考えました。
理論上はこれ以外にも、
新しい束縛条件が出てくる可能性はありますが、
現実的にはこれ以外はあまり出題されません。
もし理解が追いついていない場合は、
この2パターンを覚えてしまってもいいでしょう。
また今回は、
束縛条件のイメージが湧きやすいように、
位置、速度、加速度で考えました。
しかし実際には、
束縛条件は運動方程式と連立するため、
加速度の束縛条件だけを使う事が多いです。
ここまで難しい内容が多かったですが、
最悪以下の条件だけ覚えておけば大丈夫でしょう。
滑車 \(a_{A} = a_{B}\)
三角台 \((a_{x_{A}}+a_{x_{B}})tan\theta = a_{y_{A}}\)
まとめ
今回は束縛条件についてでした。
束縛条件は取り立てて勉強せず、
演習問題の中で現れることも多いです。
しかし運動方程式を考える上で、
未知の束縛力を処理するための考え方であり、
とても本質的な内容です。
束縛条件の考え方や意味から、
本質的に理解しておきましょう。














コメントを書く