今すぐ使える力学的エネルギー保存則！

力学的エネルギー保存則は、
力学の問題を解く中でもトップクラスで、
登場する大事な法則です。

しかし多くの受験生は、
どんなタイミングで使う法則なのか、
そもそもなぜこの法則が成り立つのか、
などを理解していないようです。

いくら言葉で理解していても、
実際の問題での「使い所」を理解していないと、
物理の実力は全く伸びません。

この記事では力学的エネルギー保存則を、
実戦で使えるように詳しく解説しますね。

この記事を読むことで、
力学的エネルギー保存則を本質的に理解でき、
さらには今すぐ問題を解き進められるようになります。

たった1つの法則を理解しただけで、
力学の解法の道筋が見えるようになるでしょう。

ぜひ最後まで読み飛ばさずに読んでみてください。

力学的エネルギー保存則とは

「力学的エネルギー」とは、
運動エネルギーと位置エネルギーを合わせたものです。

そして物体に外部から力が働かないとき、
力学的エネルギーは常に一定になります。

これを「力学的エネルギー保存則」と言います。

日本語で説明するのはとても簡単で、
力学的エネルギーは常に一定
ということです。

しかし実際に問題を解くときに、
この法則をどのように使うのかは、
具体例を見ておかないとわかりづらいですね。

次の章では力学的エネルギー保存則の使い方を確認していきます。

力学的エネルギー保存則はいつ使うのか

力学的エネルギー保存則は、
突然現れた新しい法則に見えますが、
実は運動方程式を式変形したものです。

つまり力学的エネルギー保存則は、
外部から力が加わっていなければ、
運動方程式の代わりに使うことができます。

具体例を見てみましょう。

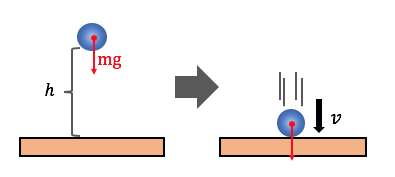
ボールを高さ\(h\)から静かに落としたとき、
地面につくときの速度\(v\)はどうなるでしょうか。

まず最初の状態では運動エネルギーはなく、
位置エネルギーだけがありますね。

　力学的エネルギー\(=0+mgh \)

次に地面にぶつかる瞬間は、
運動エネルギーだけになっています。

　力学的エネルギー\(=\frac{1}{2}mv^{2}+0 \)

そしてこれらが一定ということは、
最初と最後で力学的エネルギーが同じということですね。

\begin{align*}
0+mgh &= \frac{1}{2}mv^{2}+0 \\
v &= \sqrt{2gh}
\end{align*}

このようにエネルギーが保存しているなら、
ある2つの瞬間の力学的エネルギーを比較して、
未知の量を導くことができました。

これが基本的な使い方です。

ちなみにこの問題は、
運動方程式を使うことでも解けます。

\[ma = mg　→　a=g \]
地面に着くまでの時間を\(t\)とすると、
\[h=\frac{1}{2}gt^2　→　t=\sqrt{\frac{2h}{g}}\]
よって、\(v=gt=\sqrt{2gh}\)

力学的エネルギー保存則が成り立たない場合

力学的エネルギーが、
他のエネルギー(熱、音など)に変わってしまうとき、
もしくはエネルギーを加えられたとき、
力学的エネルギー保存則が成り立たなくなります。

エネルギーが変化する例として、
①外部から力(摩擦力など)が働く場合
②非弾性衝突の場合
があります。

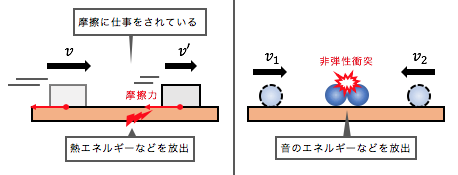
物体を手で押したり、摩擦力が足を引っ張ったり、
外部から仕事が加えられれば当然エネルギーは変化します。

また非弾性衝突では、
衝突の瞬間に「音」などのエネルギーが、
放出されることで保存則が崩れてしまいます。

①②では力学的エネルギー保存則が使えませんが、
代わりに以下の法則・定義を使います。

まずは①の例を見てみましょう。

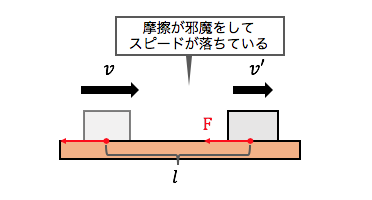
摩擦が負の仕事をすることで、
力学的エネルギー保存則が崩れています。

その代わり、摩擦の仕事に注目すれば、
以下の関係が成り立ちます。

力学的エネルギー変化＝された仕事より、
　\(\frac{1}{2}mv’^{2}-\frac{1}{2}mv^{2}=-Fl\)

エネルギーの定義は、
物体が仕事をする能力のことでしたから、
この式は定義そのままだということです。

次に②の例ですが、
詳しくは反発係数の記事を読んでください。

【合わせてチェック】
・反発係数の意味をイメージしよう！エネルギー保存則との関係まで解説

反発係数は0から1の値をとりますが、
これはどれだけエネルギーが保存しているか、
を表しています。

\(e=1\)ならエネルギーは完全に保存し、
\(e=0.5\)なら半分くらいが音や振動に変わり、
\(e=0\)なら全てが音や振動に変わって、
力学的エネルギーが全て消えています。

例えば粘土をぶつけたりすると、
ぐちゃっとくっつき全く反発しませんが、
その分、衝撃(振動)がすごいですよね。

このように反発係数は、
衝突によるエネルギー変化を表しているのです。

ちなみに\(e=1\)では、
力学的エネルギー保存則が成り立つということなので、
反発の式と力学的エネルギー保存則は同値になります。

詳しい証明は反発係数の記事をごらんください。

力学的エネルギーまとめ

力学的エネルギー関連の関係式をまとめました。

力学エネルギー保存則は、
運動方程式を式変形したものだから、
かなりの頻度で利用する法則です。

さらに保存しない場合であっても、
保存しないなりの関係式を利用します。

単に知識として保存則を覚えるのではなく、
ここまで理解しておけば、
実際の問題でも解法に迷うことはないでしょう。

応用：力学的エネルギー保存則の導出

最後に応用版として、
力学的エネルギーの保存則を導出しておきます。

できるだけ高校生向けを目指しますが、
少し大学レベルに踏み込んだ式変形もあるので、
興味がある人以外は無視して構いません。

この章を読むためには、
・速度、加速度の基本
を先に理解しておいてください。

まずは運動方程式を用意します。

\[ m\frac{dv}{dt} = F \]

いきなりわかりにくい変形ですが、
両辺に速度\(v\)を掛け算します。

これは今後の式変形を見据えた、
かなり頭のいい方法です。
\(v\)をかけて、その先の計算まで進めます。

\begin{align*}
mv\frac{dv}{dt} &= Fv\\
\int_{t_{1}}^{t_{2}}mv\frac{dv}{dt}dt &= \int_{t_{1}}^{t_{2}}Fvdt\\
\int_{v_{1}}^{v_{2}}mvdv &= \int_{t_{1}}^{t_{2}}Fvdt
\end{align*}

時刻\(t_{1}\)での位置を\(x_{1}\)、速度を\(v_{1}\)、
時刻\(t_{2}\)での位置を\(x_{2}\)、速度を\(v_{2}\)とします。

ここで\(v=dx/dt\)に注意して右辺を変形すると、

\begin{align*}
\int_{v_{1}}^{v_{2}}mvdv &= \int_{t_{1}}^{t_{2}}Fvdt \\
\int_{v_{1}}^{v_{2}}mvdv &= \int_{t_{1}}^{t_{2}}F\frac{dx}{dt}dt \\
\int_{v_{1}}^{v_{2}}mvdv &= \int_{x_{1}}^{x_{2}}Fdx \\
\frac{1}{2}mv_{2}^{2}-\frac{1}{2}mv_{1}^{1} &= \int_{x_{1}}^{x_{2}}Fdx
\end{align*}

以上により、
左辺が運動エネルギー、右辺が力による仕事、
という式になりましたね。

ここから正確に変形するには、
「保存力」と「非保存力」の考え方が必要ですが、
この辺りに関しては少しラフに考えてしまいます。

力\(F\)の中、重力や弾性力を\(F’\)、
その他の力を\(F”\)とします。
すると右辺は、

\begin{align*}
(右辺) &= \int_{x_{1}}^{x_{2}}Fdx \\
&= \int_{x_{1}}^{x_{2}}F’dx + \int_{x_{1}}^{x_{2}}F”dx\\
&= (U_{2}-U_{1}) + W
\end{align*}

となります。

重力・弾性力の仕事が位置エネルギーだから、
重力と弾性力の仕事をまとめて\(U_{1}\)、\(U_{2}\)と置いてしまいました。

その他の力による仕事は\(W\)としました。

以上から、

\begin{align*}
\frac{1}{2}mv_{2}^{2}-\frac{1}{2}mv_{1}^{1} &= (U_{2}-U_{1}) + W \\
(\frac{1}{2}mv_{2}^{2}+U_{2})&-(\frac{1}{2}mv_{1}^{1}+U_{1}) = W
\end{align*}

これによって、
エネルギー変化＝される仕事
の式が求まりました。

最後にされる仕事がない場合は、

\begin{align*}
(\frac{1}{2}mv_{2}^{2}+U_{2})&-(\frac{1}{2}mv_{1}^{1}+U_{1}) = 0 \\
\frac{1}{2}mv_{1}^{1}+U_{1}&=\frac{1}{2}mv_{2}^{2}+U_{2}
\end{align*}

となり、力学的エネルギー保存則になります。

長い道のりでしたが、
運動方程式を式変形することによって、
力学的エネルギー保存則が導けることがわかりました。

まとめ

今回は力学的エネルギー保存則の解説でした。

この記事で重要だった関係式を、
もう一度まとめておきます。

力学的エネルギー保存則は、
運動方程式を式変形して得られたもの。

だから運動方程式と同じくらい、
入試問題でも出番があります。

きっちりと練習をしておきましょう。