万有引力は、力学の最後に出て来て、
少し特殊な分野というイメージがあるかもしれません。
そのせいで、
「万有引力の問題の解き方がわからない」
「万有引力のエネルギーがわからない」
などという質問をよく受けます。
しかし実は万有引力は、
ほとんど今までの力学と同じ考え方で解けます。
あなたが万有引力の問題でつまづくのは、
万有引力を特別に考えてしまうからなのです。
ここでは、万有引力について、
簡単な例題と一緒に解説していきますね。
この記事を最後まで読めば、
万有引力の基本的な定義を深く理解でき、
問題演習でもペンがさらさら動くようになります。
では一緒に頑張っていきましょう!
目次
万有引力とは?
これまで、重力、張力、浮力、弾性力など、
さまざまな力が登場してきましたが、
高校力学で最後に習う力が「万有引力』です。
万有引力とはすべての物体同士に働く力で、
2物体の質量\(m_{1}\)、\(m_{2}\)に比例し、
2物体間の距離\(r\)の2乗に反比例するような力です。
\[F = G\frac{m_{1}m_{2}}{r^2}\](\(G=6.67×10^{-11}\)は万有引力定数)
実は今まで考えてきた物体にも、
質量があれば万有引力は生じています。
しかし万有引力定数の小ささからわかるように、
ボールや車、人間程度ではほとんど0になってしまいます。
万有引力が意味のある大きさになるのは、
惑星のようなめちゃくちゃ質量が大きい場合です。
地球が太陽の周りを回る円運動も、
万有引力が引き起こしています。
万有引力の練習問題
運動方程式のところで解説した通り、
力がわかれば運動方程式から運動を解析できるはずです。
簡単な練習問題で万有引力の練習をしてみましょう。
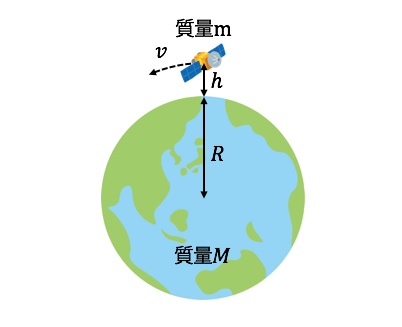
円運動の基本的な考え方がわからない場合は、
以下の記事を参考にしてください。
【合わせてチェック】
・【図解でわかる】円運動を東大院生が解説!速度・加速度の求め方
この問題も円運動の基本通り考えれば解けそうです。
まずは力の図示をしましょう。
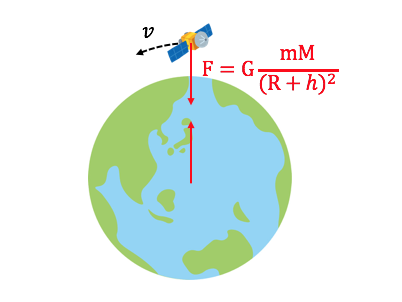
人工衛星にかかるのは万有引力だけです。
その大きさは、万有引力の定義を思い出せば、
\[ F = G\frac{mM}{(R+h)^2} \]
力がわかったので、円運動の運動方程式を立てれば\(v\)が求まります。
\begin{align*}
m\frac{v^2}{R+h} &= G\frac{mM}{(R+h)^2} \\
v^2 &= \frac{GM}{R+h}\\
v &= \sqrt{\frac{GM}{R+h}}
\end{align*}
このように万有引力もやはり力の一種なので、
運動方程式を基本に考えることができます。
万有引力と重力の関係
さて、ここで、
今まで何気なく出てきていた「重力」と、
万有引力の関係を確認しておきます。
重力はそもそも万有引力が元になって発生する力です。
より具体的に言えば、
重力とは地球と地球上の物体との間に働く、
万有引力のことを指します。
厳密には、地球上の物体の場所によって、
働く万有引力の大きさは変わりますが、
地球の半径が十分に大きいのでその差は無視できます。
つまり質量\(m\)の物体を考えれば、
以下のような関係が成り立つのです。
\begin{align*}
mg &= G\frac{mM}{R^2} \\
g &= \frac{GM}{R^2}
\end{align*}
この式は万有引力と重力加速度を結びつける式で、
頻繁に利用するものなので頭の片隅に置いておくといいでしょう。
先ほど紹介した第一宇宙速度の式は、
この関係式を利用すれば、
\[v = \sqrt{\frac{GM}{R}} = \sqrt{gR}\]
と書くことができます。
万有引力による位置エネルギー
それでは次に万有引力の位置エネルギーを考えます。
その前に、そもそもエネルギーとは、
その力によりどれだけ仕事をされたか
=どれだけ仕事をする能力があるか
を表しています。
例えば重力の位置エネルギーは、
重力\(mg\)に逆らって高さ\(h\)に持ち上げるのに、
\(mgh\)の仕事が必要だから、エネルギーは\(mgh\)です。
もしエネルギーの概念自体に不安があれば、
まずはエネルギーの復習をしておきましょう。
【合わせてチェック】
・仕事とエネルギーを解説!定義から正しく理解しよう
それでは万有引力の位置エネルギーです。
結論から言えば、
万有引力の位置エネルギーは以下のようになります。
無限遠を基準にすれば、\[U=-G\frac{mM}{r}\]
この導出は少し難しいので、
最初のうちは公式として覚えてしまってもいいかもしれません。
一応この記事では、
以下で詳しく解説していきます。
万有引力の位置エネルギーの導出
それでは万有引力の位置エネルギーの導出です。
質量\(M\)、\(m\)の2物体を用意しましょう。
この2物体が距離\(r\)のときの位置エネルギーは、
2物体を距離\(r\)の位置に持っていくのに必要な仕事に等しいです。
ということで以下のように、
2物体が同じ位置にある状態から、
質量\(m\)の方だけを引っ張って\(r\)の位置に動かしてみましょう。
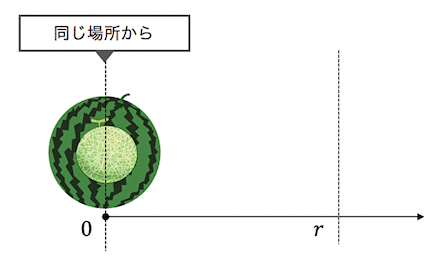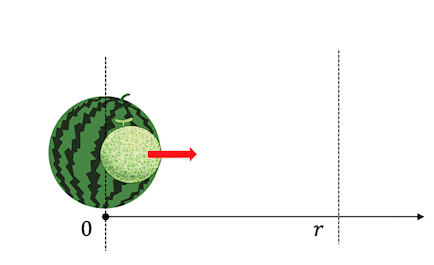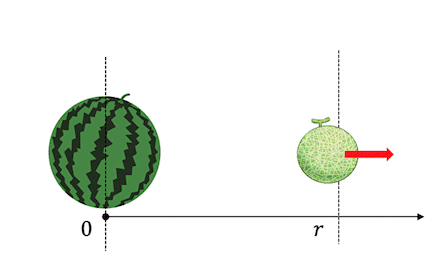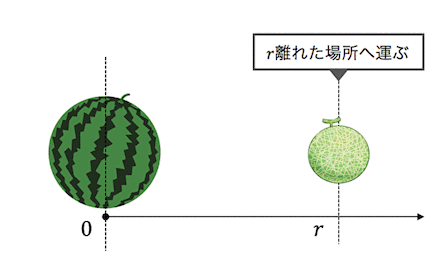
このときに必要な仕事がエネルギーとなるわけです、
が、この考え方には問題があります。
2物体が同じ位置にある場合、
万有引力が無限大に発散してしまうのです。
\[ F = G\frac{mM}{0^2} = \infty \]
そこで少し工夫をします。
位置エネルギーの基準点を変えるのです。
どういうことかわかりづらいと思うので、
一旦別の例を使って考えましょう。
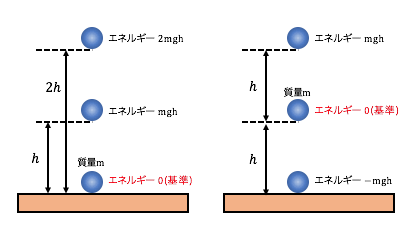
重力の位置エネルギーを考える場合、
自分で好き勝手に基準点を決めますよね。
基準点を変えたとしても、
変化の前後で同じ基準で考えれば、
基準点は好きに決めることができるのです。
そこで万有引力では、
エネルギーの基準を「無限遠」にとります。
すると無限遠から\(r\)まで運ぶ仕事は、
仕事の定義をきっちりと思い出せば、
以下のように求まります。
\begin{align*}
\int_{\infty}^{r}G\frac{mM}{r’^{2}}dr’&=\left[-G\frac{mM}{r’}\right]_{\infty}^{r}\\
&= -G\frac{mM}{r} + G\frac{mM}{\infty}\\
&= -G\frac{mM}{r}
\end{align*}
このようにして万有引力の位置エネルギーが求まりました。
さっき言った通り基準はどこでもいいので、
例えば「質量Mの物体から100m離れたところ」
などを基準に取ることもできますが、
\[ U = -G\frac{mM}{r} + G\frac{mM}{100} \]
とめんどくさそうな項が残ってしまいます。
これでも問題ないですが、
どうせなら無限遠を基準にして置いた方が、
エネルギーの式が見やすくなるのです。
例えば、富士山のてっぺんを基準に取れば、日本全国中の位置エネルギーがマイナスになります。このようにエネルギーは基準ありきのものなので、符号に本質的な意味はありません。万有引力では富士山のてっぺんどころか「無限遠」という無限に高いところを基準にしているので、エネルギーの値がマイナスになっています。
位置エネルギーの練習問題
運動方程式を使う代わりに力学的エネルギー保存則を使えば、
運動を解析することができるのでした。
【合わせてチェック】
・今すぐ使える力学的エネルギー保存則!
万有引力の位置エネルギーであっても、
基本的な考え方は一緒ではありますが、
きちんと練習をしておきましょう。
質量\(m\)の第二宇宙速度を求めよ。ただし重力加速度を\(g\)とする。
力学的エネルギー保存則を考えるときには、
変化の前後の様子をきちんと図示します。
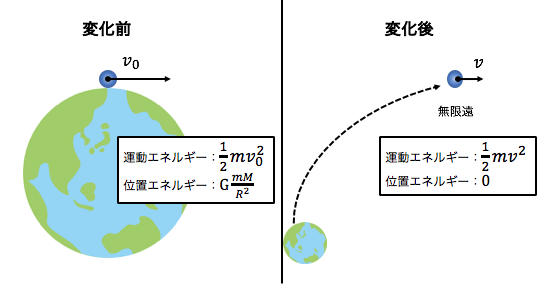
次に変化の前後でエネルギーを比較します。
\[\frac{1}{2}mv_{0}^{2}-G\frac{mM}{R} = \frac{1}{2}mv^{2}\]
無限遠でも速度を持っているためには、
\(\frac{1}{2}mv^{2}≧0\)でないといけません。
この条件を使えば、
\begin{align*}
\frac{1}{2}mv_{0}^{2}-G\frac{mM}{R} ≧ 0 \\
v_{0} ≧ \sqrt{\frac{2GM}{R}} = \sqrt{2gR}
\end{align*}
最後の変形では、\(g=\frac{GM}{R^2}\)を使いました。
以上より、\(\sqrt{2gR}\)以上の初速があれば、
地球の重力を振り切ることができるので、
第二宇宙速度は\(\sqrt{2gR}\)となります。
慣れないと少し難しく感じますが、
やっていることはただのエネルギー保存則です。
参考:ケプラーの法則
(準備中です。)
まとめ
今回は万有引力の解説でした。
必要な知識をまとめておきます。
万有引力の位置エネルギー\[U = -G\frac{mM}{r}\]
第一宇宙速度
地表スレスレを等速円運動するときの速度。
第二宇宙速度
地球の重力を振り切るのに必要な初速。
万有引力はとっつきにくいイメージがありますが、
解法は意外と今までの力学と同じ部分が多いです。
きっちりと練習しておきましょう。













コメントを書く