「慣性力をいつ使えばいいのかわからない」
「『見かけの力』ってなに?」
「向心力と遠心力の違いは?」
慣性力は高校の力学の中でも、
概念として理解するのが難しく、
苦労する人も多いですね。
問題で慣性力を使う場合も、
なんとなーく使っている人が多いでしょう。
あなたが慣性力をうまく扱えないのは、
慣性力が『なぜ』使われているのかが、
明確ではないからです。
ここでは慣性力の解説を行います。
この記事を最後まで読むことで、
慣性力を使う理由、慣性力の意味を理解でき、
入試問題でも迷いなく使えるようになります。
慣性力を曖昧に理解していると、
円運動などの別の分野にも影響が出てきます。
ぜひ最後まで読み飛ばさずに読んでみてください。
目次
運動方程式が成り立たない!?
突然ですが、
電車で急ブレーキがかかったとき、
を想像してみてください。
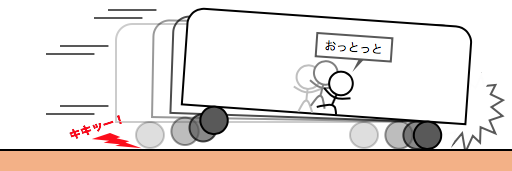
電車で急ブレーキがかかれば、
体がよろけて倒れそうになりますよね。
しかしよーく考えてみると、
電車の中の人は誰かに押されたわけでも、
引っ張られたわけでもありません。
つまり何も力がないのに、
勝手に体が動いてしまっているのです。
力が無いのに加速したということは、
運動方程式が成り立っていないということです。
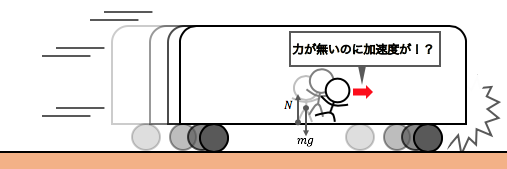
でも少し考え直して、
急ブレーキするのを駅のホームで見ていたとしましょう。
そうすると問題はもう少しシンプルです。
初めは電車と人間が同じスピードで動いていて、
急ブレーキをかけると電車だけが減速し、
そして人間だけが先に行ってしまう。
つまり人間が引っ張られたのではなく、
電車自体が逆方向に動いたのです。
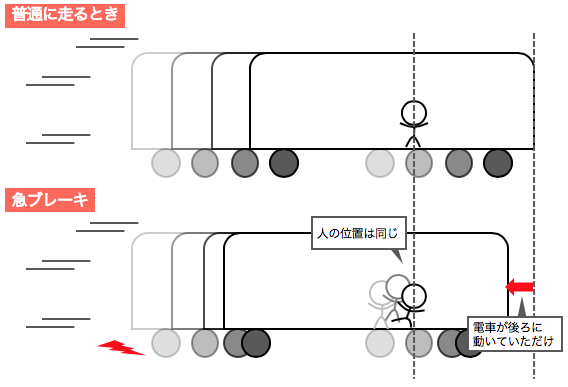
以上の例からわかるように、
電車の中にいる人の目線で考えるか、
駅にいる人の目線で考えるかによって、
見方が変わってきます。
見方の違いによって、
運動方程式が成り立たない場合もあるのです。
先ほどの駅からの目線のように、
運動方程式が成り立つ目線を「慣性系」と呼びます。
逆に電車の中からの目線のように、
運動方程式が成り立たない目線を「非慣性系」と呼びます。
同じ運動であっても、
どこから見るか(=観測者の位置)によって、
考え方が変わってしまうのです。
ではどんな場合が非慣性系かというと、
・観測者が加速度運動をしている場合
・観測者が円運動をしている場合
です。
そして非慣性系でなければ必ず慣性系です。
…
でも、
運動方程式が使えない時もある、
ではなんか嫌ですよね。
いつでも運動方程式で解ける!
という方が理想です。
実はそんなワガママを実現するのが「慣性力」です。
慣性力は非慣性系を慣性系に変える
先ほどの電車の例では、
急ブレーキで人間が動いてしまった原因は、
電車が後ろ向きの加速度を持ったからです。
それによって電車内の人間は、
相対的に前向きの加速度を持ったのでした。
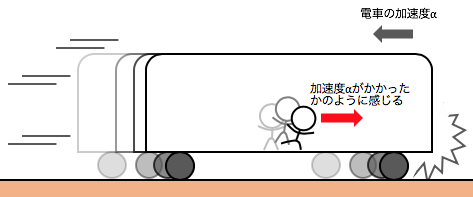
ではこのように考えてみましょう。
電車の後ろ向きの加速度を\(\alpha\)として、
電車が急ブレーキしたとき、
人間に前向きに\(m\alpha\)の力がかかったと「仮定」します。
すると人間は確かに、
前向きに加速度\(\alpha\)を持つことになります。
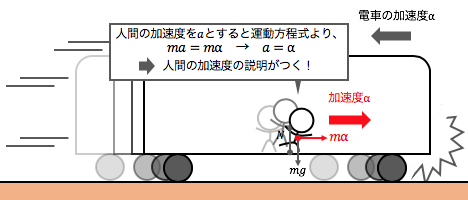
このように、非慣性系であっても、
勝手に力がかかっていると仮定してしまえば、
運動方程式が使えるようになるのです。
この力のことを「慣性力」と言います。
別の表現をすれば、
慣性力という見かけの力を考えれば、
非慣性系を慣性系に変換できるということです。
話をうまく進めるための「仮定の力」だと思っておきましょう。慣性力は見かけの力だから、普通の力と違って反作用が働いていません。
今までの説明をまとめれば以下の通り。
慣性系 運動方程式が成り立つ
非慣性系 運動方程式が成り立たない
→慣性力を導入すると慣性系に
結局のところ、慣性力をマスターすれば、
どんな場合でも運動方程式が使えるということ。
これはとても便利ですね。
これでどんな観測者から見ても、
運動方程式で問題を考えることができます。
次に今一度、慣性力とはどんなものか、
①観測者が加速度運動をしている場合
②観測者が円運動をしている場合
に分けて解説していきます。
①観測者が加速度運動をしている場合
観測者が加速度運動している場合、
物体には逆向きの加速度がかかって見えます。
そのため観測者が加速度\(\alpha\)で運動するとき、
質量\(m\)の物体には\(-m\alpha\)の「慣性力」がかかると考えます。
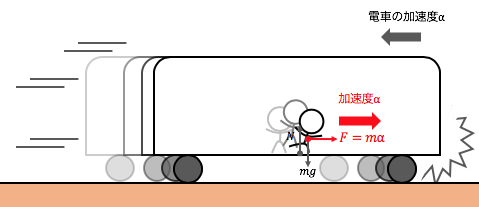
これは電車の例で説明した通りです。
②観測者が円運動をしている場合
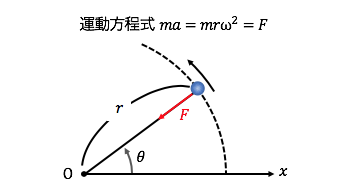
物体が円運動している場合、
物体には円の中心に向かって、
\(r\omega^2\)の加速度がかかっています。
この辺りが曖昧な場合は、
以下の記事を参考にしてみてください。
【合わせてチェック】
・【図解でわかる】円運動を東大院生が解説!速度・加速度の求め方
円運動する物体には\(r\omega^2\)の加速度がかかります。
つまりその物体に観測者がいたら、
物体ばっかり加速度がかかっているため、
観測者を取り残して円運動してしまいます。
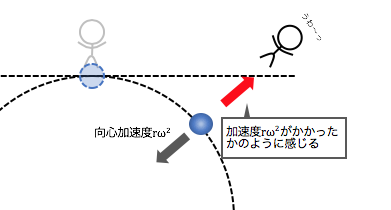
これも先ほど同様見方を変えれば、
質量\(m\)の観測者に\(mr\omega^2\)の「慣性力」がかかったと考えられます。
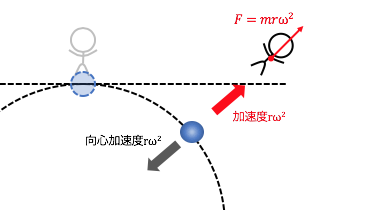
このように円運動であっても、
やはり加速度が生じてしまっている影響で、
逆向きの慣性力を考える必要があるのです。
慣性力の練習問題
問題
(2)図2のように、長さ\(l\)の糸に質量\(m\)のボールを吊るし、鉛直線と糸がなす角が\(\theta\)となるように、水平面内で等速円運動をさせたとき、円運動の周期を求めよ。ただし重力加速度を\(g\)とする。
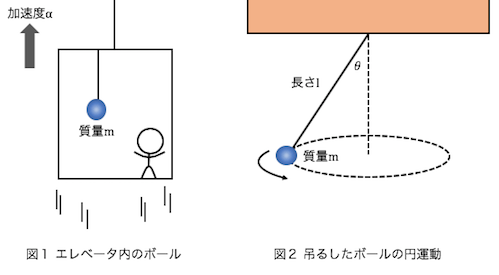
解答
(1)
エレベータが止まっている場合は、
重力\(\mg)だけがかかりますが、
エレベータの加速度運動によって慣性力もかかります。
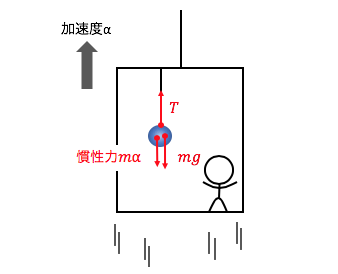
あとはエレベータ内部の観測者を考え、
力の釣り合いを考えると以下の通り。
\begin{align*}
0 &= mg + ma – T \\
T &= m(g+a)
\end{align*}
(2)
実はこの問題は、
・円運動の運動方程式で解く方法
・慣性力を考え、力の釣り合いで解く方法
の2通りがあります。
今回は慣性力の記事ですが、
理解をより深めるために、まずは、
円運動として考える方法から解説します。
それではまずは、
この運動を外から見る観測者を考えて、
図示してみます。
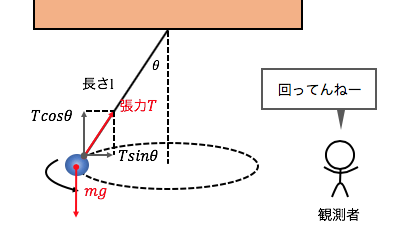
鉛直方向では力の釣り合いを、
垂直方向では円運動の運動方程式を考えると、
\begin{align*}
0 &= Tcos\theta – mg \\
m(lsin\theta)\omega^{2} &= Tsin\theta \\
(半径r&=lsin\thetaに注意)
\end{align*}
以上より\(\omega=\sqrt{\frac{g}{lcos\theta}}\)となるので、
周期は\(T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{lcos\theta}{g}}\)となります。
次に慣性力を使った解法です。
ボールと一緒に動く観測者を考え、
力の図示をします。
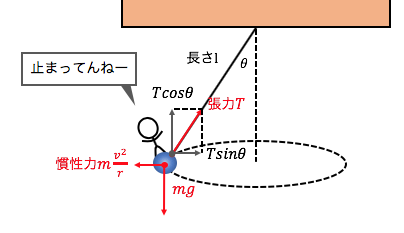
今、ボールの上の観測者を考えているので、
観測者から見たらボールは止まっています。
地球の上にいる僕たちが、
地球の公転を感じられないのと同じです。
つまりボールの上の観測者では、
ボールが完全に静止して見えるので、
鉛直、水平方向で両方力の釣り合いが成り立ちます。
\begin{align*}
0 &= Tcos\theta – mg \\
0 &= Tsin\theta – m(lcos\theta)\omega^{2} \\
よって\omega&=\sqrt{\frac{g}{lcos\theta}}であり、\\
周期はT&=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{lcos\theta}{g}}
\end{align*}
当然ながら先ほどと同じ答えです。
【合わせてチェック】
・【図解でわかる】円運動を東大院生が解説!速度・加速度の求め方
まとめ
今回は慣性力の解説でした。
まず運動方程式を立てるに当たって、
観測者の立ち位置によって、
「慣性系」と「非慣性系」がありました。
非慣性系では運動方程式が成り立たないですが、
「慣性力」を使えば慣性系に変換できるのでした。
慣性系 運動方程式が成り立つ
非慣性系 運動方程式が成り立たない
→慣性力を導入すると慣性系に
これによって、
全ての運動で運動方程式で成り立つ
ということができるのです。
これを前提に、
・観測者が加速度運動を行う場合
・観測者が円運動を行う場合
の慣性力を考えました。
どちらも本質は変わらず、
加速度を打ち消すような力を、
導入すればよかったですね。
実際に慣性力を使いこなすには、
問題演習をするのが一番なので、
ぜひ手元の問題集で練習してみてください。














半径r=lsinθではないでしょうか?
ミスっちゃってましたね…、ご指摘ありがとうございます!