万有引力はなんとなく理解できたけど、
ケプラーの法則がよくわからない。
なんとなく言っていることはわかるけど、
実際の問題での使い方がわからない。
あなたもそんなふうに思っていませんか?
ケプラーの法則はとっつきづらく、
あまり問題にも出くわさないため、
意外と苦手なままだったりしますよね。
あなたがケプラーの法則を使えないのは、
単に使い方を意識的に勉強していないからです。
ここではケプラーの法則を、
その意味と使い方を合わせて解説しますね。
この記事を読み、例題を解けば、
ケプラーの法則の意味や使いどころが、
スッキリ理解できます。
ぜひ最後まで読んでみてください。
目次
惑星の運動はほんとは楕円軌道
万有引力の解説や例題では、
主に万有引力による円運動を考えました。
しかしこれはあくまで特別な場合で、
一般に万有引力による惑星などの運動は、
楕円軌道上を動きます。
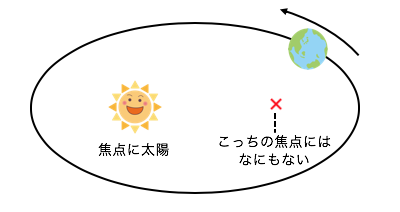
実はこれは、万有引力の式、
\[ F = G\frac{mM}{r^{2}} \]
から導出することができるのですが、
万有引力の発見以前にこれを発見したのが、
「ヨハネス・ケプラー」先生です。
ケプラーは火星の観察記録を見て、
惑星の運動に関する考察をしました。
その結果導き出されたのが「ケプラーの法則」です。
今回はそんなケプラーの法則を勉強していきましょう。
ケプラーの法則
それでは早速、「ケプラーの法則」を列挙します。
第1法則:楕円軌道の法則
惑星は太陽を焦点とする楕円上を運動する。
第2法則:面積速度一定の法則
惑星と太陽を結ぶ線分が単位時間当たりに描く面積(面積速度)は一定である。
第3法則:調和の法則
惑星の公転周期の2乗は、軌道長半径の3乗に比例する。
これだけでは少し理解しづらいので、
それぞれ個別に確認していきます。
第1法則:楕円軌道の法則
惑星は太陽を焦点とする楕円上を運動する。
第1法則の楕円軌道の法則はその名の通り、
惑星は楕円運動をするという法則です。
そして太陽がその楕円運動の焦点になります。

万有引力のように距離の2乗に反比例する力の場合、
数学的に計算すると楕円軌道になることがわかります。
この計算は高校レベルを超えるので、
この記事の最後に参考程度に触れます。
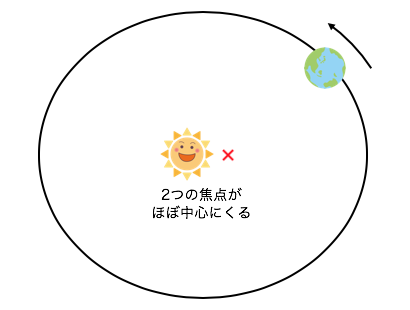
ちなみに地球も楕円軌道で公転するとはいえ、
焦点が中心に非常に近いために、
ほとんど円運動のようになっています。
第2法則:面積速度一定の法則
惑星と太陽を結ぶ線分が単位時間当たりに描く面積(面積速度)は一定である。
「面積速度」という言葉は聞きなれないので、
まずは図を見て確認してみます。
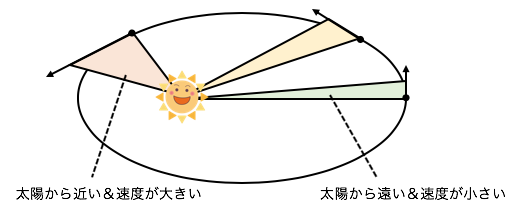
楕円運動では、
太陽から近くにあるときほど速く、
太陽から遠くにあるときほど遅く動きます。
その結果、太陽と惑星の軌道が単位時間に作る、
扇型の面積が等しい、というのが第2法則です。
それでは面積速度を数式で考えてみましょう。
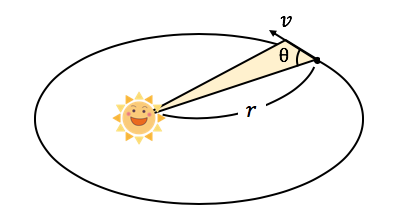
三角形の面積公式より、
\[ 面積速度 = \frac{1}{2}rvsin\theta \]
式自体を覚える必要はありませんが、
この式から面積速度の意味を理解できるといいと思います。
第3法則:調和の法則
惑星の公転周期Tの2乗は、軌道長半径aの3乗に比例する。
式で表すなら、
\[ \frac{T^{2}}{a^{3}} = 一定 (T^{2}=ka^{3})\]
です。
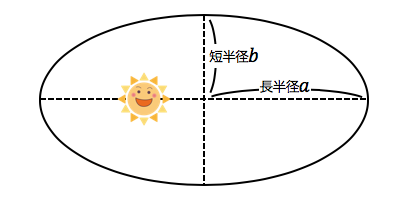
ちなみに軌道長半径とは、
した図のように楕円軌道の長い半径のことです。
この式も導出自体は可能ですが、
直感的に理解するのも難しい式なため、
覚えてしまうのがいいと思います。
ただここで注意しておきたいのは、
定数kは焦点になる物体に依存することです。
つまり太陽系の惑星同士は同じになるし、
地球の人工衛星同士も同じになりますが、
惑星と人工衛星では異なる値になります。
第3法則を実際に使うときは、
kを与えられない場合が多いため、
複数の惑星を比較して使います。
これらについても次の例題で練習していきましょう。
ケプラーの法則ってどうやって使うの?
ケプラーの法則の難しいところは、
使いどころがわかりづらいことでしょう。
ここでは実際の例題を使って、
使い方の練習をしていきます。
ここで、前提を確認しておきましょう。
そもそもケプラーの法則は、
万有引力の法則を使えば全て証明できます。
そういう意味ではケプラーの法則をただの「公式」です。
ということは万有引力さえあれば、
本当はケプラーの法則を考えなくても、
惑星の運動を計算することができるということです。
しかしそのためには、
大学の数学知識が必要になるのです。
楕円軌道が難しいせいですね。
そんなときに便利なのがケプラーの法則。
ケプラーの法則を「公式」として使えば、
難しい楕円軌道も考えることができます。
これを前提に考えておくと、
惑星の運動の問題が出てきた時にも、
解法に迷いづらいと思います。
さて、前提が共有できたところで、
例題をみていきましょう。
例題
地球の質量を\(M\)、半径を\(R\)、万有引力定数を\(G\)とする。
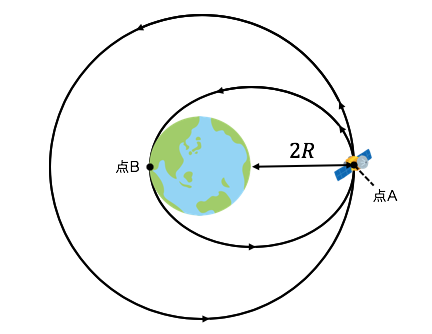
(1)地上\(2R\)の円軌道上を人工衛星が回っている。その速さ\(v\)と周期\(T_{0}\)を求めよ。
(2)人工衛星を図の点Aで減速させて楕円軌道に乗せ、地表の点Bで回収したい。点A、点Bでの速度\(v_{A}\)、\(v_{B}\)をそれぞれ求めよ。
(3)減速してから人工衛星が回収されるまでの時間を求めよ。
ヒント:
(1)単に円軌道を回っている場合は、
万有引力を使えば良いのでした。
(2)楕円軌道になったらケプラーの法則の出番。
(3)回収されるまでの時間は、楕円軌道の周期の半分ですね。周期を求めるには?
解答
(1)円運動であれば、何も恐れることはありません。
単に万有引力で円運動を考えるだけです。
半径\(3R\)の等速円運動だから、
速さを\(v\)、人工衛星の質量を\(m\)とすれば、
円運動の運動方程式より、
\begin{align*}
m\frac{v^{2}}{3R} &= G\frac{mM}{(3R)^{2}} \\
v &= \sqrt{\frac{GM}{3R}}
\end{align*}
周期\(T_{0}\)は、
\begin{align*}
T_{0} &= \frac{2\pi (3R)}{v} \\
&= 6\pi R\sqrt{\frac{3R}{GM}}
\end{align*}
(2)楕円軌道を考えるとなれば、
ケプラーの法則の出番です。
今回の問題の点Aと点Bは、
両方軌道に対して90°向きに速度を持つので、
面積速度は以下の直角三角形の面積です。
よって第2法則が使いやすいですね。
\[ \frac{1}{2}Rv_{B} = \frac{1}{2}(3R)v_{A} \]
しかしこれだけでは、
変数2つに対して式1つで解けないので、
エネルギー保存則も使ってあげましょう。。
\[ \frac{1}{2}mv_{B}^2 – G\frac{mM}{R} = \frac{1}{2}mv_{A}^2 – G\frac{mM}{3R} \]
2つの式を連立して解けば、
\[ v_{A} = \sqrt{\frac{GM}{6R}}、 v_{B} = \sqrt{\frac{3GM}{2R}}\]
(3)ヒントにも書いた通り、
点Aから点Bにたどり着くのには、
楕円周期の半分の時間がかかります。
ということは周期を求めればいいのですが、
楕円軌道を運動する周期を求めるのは、
高校レベルでは難しいです。
そこで使われるのがケプラーの第3法則です。
楕円軌道の周期を\(T\)として、
楕円の長半径\((R+3R)/2R=2R\)に注意すると、
\begin{align*}
\frac{T^{2}}{(2R)^{3}} &= \frac{T_{0}^{2}}{(3R)^{3}} \\
T &= (\frac{2}{3})^{\frac{3}{2}}T_{0}
\end{align*}
AB間は半周期で動けるから
\begin{align*}
\frac{1}{2} &= \frac{1}{2}\cdot(\frac{2}{3})^{\frac{3}{2}}\cdot 6\pi R\sqrt{\frac{3R}{GM}} \\
&= 2\pi R\sqrt{\frac{2R}{GM}}
\end{align*}
参考:ケプラーの法則の導出(準備中)
参考としてケプラーの法則の導出をします。
大学入試的には全く必要がないので、
興味がない人はここは読まなくても大丈夫です。
また、本当は受験生にも配慮したいですが、
数学・物理の難易度的にどうしても
大学レベルの内容になってしまいます。
受験生だけど気になる!という人は、
「わからないけど理解してみたいな!」
という気持ちで眺めてもらえればと思います。
第2法則の導出
剛体の力学の記事でも説明した通り、
高校物理では回転運動を少ししか勉強しません。
水平運動における力に相当するものが、
回転運動におけるモーメントだったように、
回転運動の中にも水平運動に相当するような、
概念がいくつか出てきます。
そんな中で、水平運動の運動量に相当するのが、「角運動量」です。
位置\(\vec{r}\)、運動量\(\vec{p}\)の物体の角運動量は、
\[ \vec{L} = \vec{r}\times\vec{p} \]
と「外積」を使って定義されます。
ここで、角運動量の時間微分を考えると、
\begin{align*}
\frac{d\vec{L}}{dt} &= \frac{d}{dt}(\vec{r}\times\vec{p})\\
&= \frac{d\vec{r}}{dt}\times\vec{p} + \vec{r}\times\frac{d\vec{p}}{dt} \\
&= \vec{v}\times\vec{p} + \vec{r}\times\vec{F}
\end{align*}
外積の性質として、
同じ向きのベクトルの外積が0になる
ということが知られています。
よって\(\vec{v}\times\vec{p}=0\)であり、
万有引力という中心力が働く場合は、
位置と力も平行になるので\(\vec{r}\times\vec{F}=0\)です。
以上から、
\[\frac{d\vec{L}}{dt}=0\]
つまり、角運動量は時間に依存しない、
=角運動量保存則が導けました。
中心力による回転運動の場合は、
角運動量が保存するということです。
さてここで、下図の惑星を考えます。
[画像]
外積の定義に基づいて計算すれば、角運動量の大きさLは、
\begin{align*}
L &= rpsin\theta \\
&= mrvsin\theta
\end{align*}
ここで先ほどの面積速度\(A=\frac{1}{2}rvsin\theta\)を思い出せば、
\begin{align*}
L &= mrvsin\theta \\
&= 2mA \\
A &= \frac{L}{2m} = 一定
\end{align*}
角運動量保存則から、面積速度一定とわかりました。
第3法則の導出
(準備中)
第1法則の導出
(準備中)
まとめ
今回はケプラーの法則の解説でした。
ケプラーの法則をまとめておきましょう。
第1法則:楕円軌道の法則
惑星は太陽を焦点とする楕円上を運動する。
第2法則:面積速度一定の法則
惑星と太陽を結ぶ線分が単位時間当たりに描く面積(面積速度\(=\frac{1}{2}rvsin\theta\))は一定である。
第3法則:調和の法則
惑星の公転周期\(T\)と軌道長半径\(a\)は、\(T^{2}=ka^{3}\)を満たす。ただし\(k\)は、焦点の物体に依存する定数である。
これらは具体的な問題の解き方と合わせて
理解した方がいいでしょう。
例題が理解できなかった人は、
ぜひ時間をかけて考えてみてください。













コメントを書く