運動量や力積の意味を説明できますか?
また、どんなときに運動量保存則を使うのか、
その「使い所」を説明できますか?
物理を得意としている受験生でも、
意外とこのあたりは盲点になりやすいです。
でも冷静に考えれば、
運動量保存則の使い所を理解していないと、
実際の問題で使いこなすことは難しいです。
あなたが運動量保存則を使いこなせないのは、
運動量保存則の意味を本質的に理解できていないからです。
この記事では運動量や力積の定義、
そして運動量保存則について本質的に解説していきます。
この記事を最後まで読むことで、
運動量保存則がどんな法則なのかがわかり、
実際の入試問題でも自由に使えるようになります。
今までわかった気になっていた部分も、
すっきりと理解できると思います。
ぜひ最後まで読み飛ばさずに読んでみてください。
目次
運動量と力積とは?
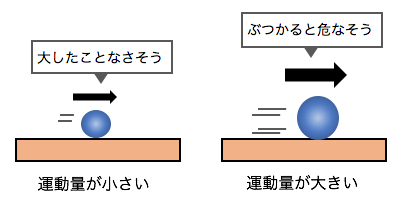
「運動量」を一言でいうなら、
物体の運動の激しさを表す量です。
車でイメージすると、
ただスピードが早いだけでなく、
トラックのような重たい車の方が、
ぶつかったときの衝撃がすごそうです。
この衝撃の強さ=運動の激しさが運動量です。
次に「力積」を一言でいうなら、
運動量を変化させるための量です。
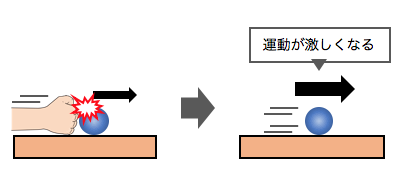
例えば転がっているボールの運動量を増やして、
さらに激しく運動させたいとしましょう。
そんなときには、
ボールを手で押してあげることで、
力積を与えればよいのです。
つまり運動の激しさが運動量で、
運動の激しさを変化させるのが力積なのです。
以下ではこの運動量と力積を、
もう少し詳しく考えていきましょう。
運動量の意味と定義
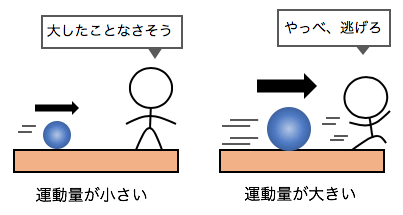
例えば、ボールがぶつかってくるのを
想像してみましょう。
ボールが重ければ重いほど、
ボールが速ければ速いほど、
ぶつかると痛そうですよね。
このように、
運動量\(p\)は物体の質量\(m\)と速度\(v\)に比例し、
以下のように表されます。
ここで運動量には「向き」があることに
注意しておきましょう。
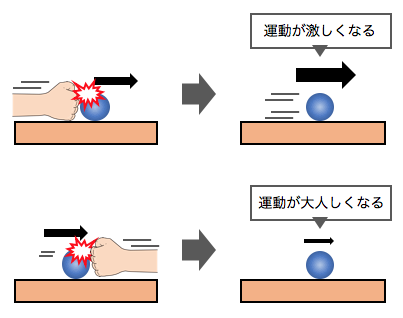
転がるボールを後ろから押せば、
運動がさらに激しくなりますが、
同じように前から押せば、
ボールは徐々に止まっていきます。
つまりボールは右向きの運動量を持っていたということです。
運動量の定義 \(\vec{p}=m\vec{v}\)
力積の意味と定義
ボールを押して運動量を増やしたいとき
強い力で長い時間押した方が良さそうですね。
よって、力積\(\vec{I}\)は、
力\(\vec{F}\)と力をかける時間\(\Delta t\)に比例し、
以下のように表されます。
しかし、(仮)と書いたように、
この定義は正確ではありません。
なぜかというと、力をかけている間に、
力も刻一刻と変化することがあるからです。
例えば\(t_{A}\)秒から\(t_{B}\)秒までの\(\Delta t = t_{B}-t_{A}\)秒間、
以下のグラフのように力が変化したとしましょう。
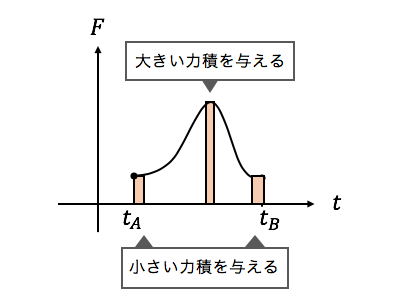
最初のうちは小さめな力で、
途中ではかなり大きな力で、
最後はまた小さな力で押しているようです。
これは速度・加速度の記事の方法を思い出せば、
グラフの面積の部分が力積になるとわかります。
つまり力積の定義は以下の通り。
力を時間的に積み重ねたものが、
力積になっているのです。
運動量と力積の関係
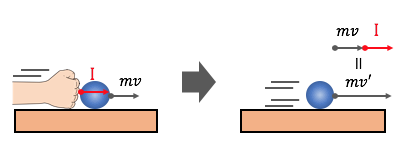
最初に説明した通り、
力積は運動量を変化させるためのものです。
これを式にまとめると以下の通り。
これを日本語で読めば、
運動量の変化は力積に等しい
となります。
この関係式は力積の意味をよく表しているので、
先ほどの式ではなくこちらを定義として、
理解しておいてもいいでしょう。
実はこの関係式は、
運動方程式を同値変形して得られるのです。
ただし一応高校範囲を超えるので、
詳しい解説は「応用」として最後に解説します。
運動量保存則
次に「運動量保存則」の解説です。
まずは2つのボールの衝突を考えてみましょう。
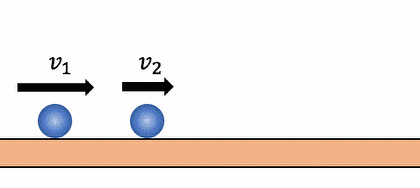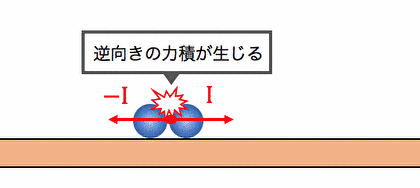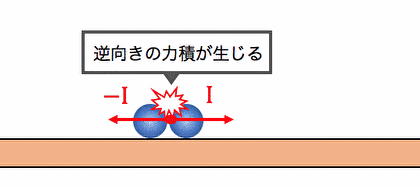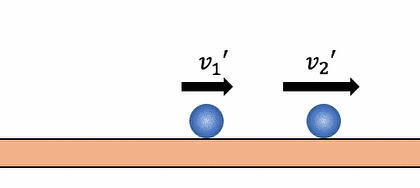
2つのボールが衝突をしている瞬間、
「作用反作用の法則」に従って、
お互いに逆向きの力を掛け合っています。
つまり力積の定義を思い出せば、
ボールは逆向き、同じ大きさの力積を与えています。
これに注意して、
2つのボールについて運動量変化を考えると以下。
\begin{align*}
m_{1}v’_{1} – m_{1}v_{1} &= I \\
m_{2}v’_{2} – m_{2}v_{2} &= -I
\end{align*}
この式からIを消去すると、
\begin{align*}
m_{1}v’_{1} – m_{1}v_{1} &= m_{2}v’_{2} – m_{2}v_{2} \\
m_{1}v_{1} + m_{2}v_{2} &= m_{1}v’_{1} + m_{2}v’_{2}
\end{align*}
となって、2つのボールの運動量の合計が、
衝突の前後で変わりません。
これを「運動量保存則」と呼びます。
運動量保存則は、
力学の問題を解いていく中で、
とても重要でとても頻繁に使う法則です。
なぜ運動量保存則が重要か、
について詳しく説明しておきましょう。
なぜ運動量保存則が重要か
結論から言えば以下の2つの理由があります。
理由① 力がわからなくても使える
理由② 運動方程式と同値である
ここまで何度も言ってきたように、
力学の問題は運動方程式がすべてです。
だから原理上は、
運動方程式を使えばどんな問題も解けます。
しかし先ほどの衝突を思い出しましょう。
2つのボールが衝突するとき、
力Fがどんな力かがわかりませんでした。
これでは運動方程式を立てることができません。
そこで使うのが運動量保存則。
運動量保存則は、運動方程式と同値なので、
運動方程式の代わりに使えます。
しかも力を知らなくても使えます。
よって運動量保存則は、
運動方程式がうまく使えない時に、
その代わりに使われる法則なのです。
だからこそとっても重要な法則なんですね。
運動量保存則の注意点
運動量保存則が成り立つのは、
外から力が生じていない場合のみです。
当たり前ですが、
外から力積が加えられれば、
運動量の変化が起こってしまいます。
注目した物体同士以外に、
運動量を変化させる力積がない場合のみ、
運動量保存則が成り立ちます。
応用:運動量保存則の導出
最後に応用として、
運動量保存則の導出をしておきましょう。
興味がない人は飛ばしてしまって構いません。
ただ導出と言っても、
・速度、加速度の意味
・運動方程式の意味
をきちんと理解できていればすぐに求まります。
【合わせてチェック】
・超重要!位置・速度・加速度を理解しよう!【高校物理】
・力学の最重要法則「運動方程式」で未来を予知する
では、1つの物体に対して運動方程式を立てます。
\[ m\frac{dv}{dt} = F \]
そろそろこの加速度の書き方にも慣れたでしょうか。
次にこの両辺をtで積分します。
時刻\(t_{A}\)での速度が\(v\)、時刻\(t_{B}\)での速度が\(v’\)とすると
\begin{align*}
\int_{t_{A}}^{t_{B}}m\frac{dv}{dt}dt &= \int_{t_{A}}^{t_{B}}Fdt \\
\int_{v}^{v’}mdv &= \int_{t_{A}}^{t_{B}}Fdt \\
mv’ – mv &= \int_{t_{A}}^{t_{B}}Fdt
\end{align*}
このようにして、
力積と運動量の関係が得られました。
ここまでくれば2物体の運動量保存則の証明は、
運動量保存則の章の中で書いた通りです。
まとめ
今回出てきた定義、法則をまとめましょう。
運動量 \( \vec{p} = m\vec{v} \)
力積 \( \vec{I} = \int \vec{F}dt \)
法則
運動量と力積 \(mv’ – mv = \int_{t_{A}}^{t_{B}}Fdt\)
運動量保存則 \(m_{1}v_{1} + m_{2}v_{2} = m_{1}v’_{1} + m_{2}v’_{2} \)
まずはこれらをしっかり押さえましょう。
その上でより大事なのは、
運動量保存則の使いどきを理解することです。
運動方程式と同値である運動量保存則は、
生じる力がわかりにくい衝突の問題などで、
運動方程式の代わりに使われるのでしたね。
ぜひ実際の問題で使えるように、
この事実から理解しておきましょう。














コメントを書く