高校物理の力学で最も重要なのは、
間違いなく運動方程式です。
しかし多くの受験生は以下の状態に陥りがちです。
⚫︎ 運動方程式を使うタイミングがわからない
⚫︎ 運動方程式の重要性が理解できない
etc…
これらの問題によって、
そもそも力学全体の理解度が下がってしまいます。
この記事は、運動方程式の解説です。
この記事を最後まで読むことで、
運動方程式を本質的に理解することができ、
問題の解法が簡単に頭に浮かぶようになるでしょう。
特に後半は、
物理が少し得意な人向けの内容です。
ぜひ最後まで読んでみてください。
目次
運動方程式で未来予知
「運動方程式」は\(ma=F\)と非常に単純な形をしていて、
一見その意味がわかりづらいかもしれません。
しかし実は、
運動方程式は未来を予知することができる、
とてもすごい式なんです。
なぜそんなことが言えるか、
もう一度運動方程式を見てみましょう。
運動方程式\(ma=F\)を日本語で読むなら、
「力の分だけ、加速度が生じるよ」
となります。
これがとってもすごいことなんです。
加速度は「速度の変化具合」ですから、
加速度がわかれば速度がわかります。
そして速度は「位置の変化具合」ですから、
速度がわかれば位置がわかります。
以上をぜーんぶ足して考えれば、
力のかかり方がわかれば、物の位置を予想できる
ということになります。
少しすごさがわかってきましたか？
より詳しい運動方程式の使い方
もう少しきっちりと考えてみましょう。
運動方程式をきっちり理解するためには、
「加速度」を理解する必要があります。
それについては以下の記事で詳しく説明しています。
【合わせてチェック】
・超重要！位置・速度・加速度を理解しよう！【高校物理】
簡単に復習すると、
速度は、位置の変化率＝位置\(x\)の時間微分、
加速度は、速度の変化率＝速度\(v\)の時間微分、
ということは位置の二階微分でしたね。
これを裏返せば、
運動方程式を二回積分することで、
位置が時間の関数として求まるのです。
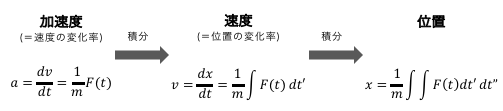
ただし毎回積分するのは大変なので、
よく出てくる運動には公式が用意されています。
\[ x = x_{0} + vt \]
等加速度運動(\(a=一定\)のとき)\begin{align*}
v &= v_{0} + at \\
x &= x_{0} + v_{0}t + \frac{1}{2}at^{2}
\end{align*}
現実的にはここまで理解していなくても、
公式の使い方さえ押さえておけば問題は解けます。
しかし運動方程式をきっちり理解すると、
起こっている現象がイメージしやすくなり、
力学の理解の助けになるでしょう。
練習問題「鉛直投射」
それではいくつか練習問題を解いてみます。
運動方程式を使って問題を解く流れは、
①力の図示をすることで力Fを求める
②運動方程式を立てる
③公式や積分計算で位置を求める
となります。
この中の「力の図示」に関しては、
以下で詳しく解説しています。
【合わせてチェック】
・たった2STEPでできる！力の図示のコツ
今回は運動方程式に集中するため、
②③にしぼって考えられる練習問題です。
問題
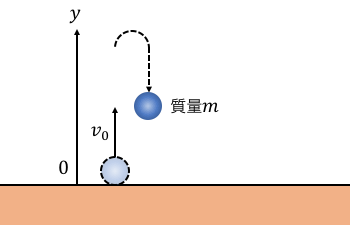
解答
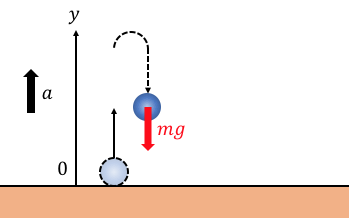
力は簡単に図示できると思うので、
上向きを正として運動方程式を立てましょう。
\begin{align*}
ma &= -mg \\
a &= -g (=一定)
\end{align*}
まずは等加速度運動の公式で解いてみます。
初期条件は高さが0、速度が\(v_{0}\)だから、
\[ y = v_{0}t – \frac{1}{2}gt^{2} \]
このように答えが求まりました。
仮に積分で解いてみるなら、
以下のようになります。
\begin{align*}
m\frac{d^{2}y}{dt^{2}} &= -mg \\
\frac{d^{2}y}{dt^{2}} &= -g \\
\frac{dy}{dy} &= -gt+C \\
y &= -\frac{1}{2}gt^2+Ct+C’\\
(ただし&C、C’は積分定数)
\end{align*}
\(t=0\)で高さ\(y=0\)、速度\(dy/dt=v_{0}\)より、
\[ y = v_{0}t – \frac{1}{2}gt^{2} \]
運動方程式でうまく解けない場合
「運動方程式で未来がわかる」と言われても、
実際の問題はいつもここまで単純じゃありません。
その原因はいくつかありますが、
主に物理学的な問題と高校物理の問題に分けられます。
まだ運動方程式を習ったばかりであれば、
この章は発展的なので飛ばしてしまいましょう。
ただ一通り力学を学んだ人にとっては、
この記事の中でもっとも重要な内容です。
まずは物理学的な問題から見ていきます。
物理学的な問題①「非慣性系」
実は運動方程式は、
どんなときでも成り立つわけではありません。
未来予知できるとか騙したのか！！
なんて言わないでください 笑
今からちゃんと説明します。
まず「座標系」について説明します。
例えば車の中で座って静止していても、
車の外にいる人からすれば車と一緒に動いて見えます。
このように物理現象は見方によって代わり、
この「見方」のことを「座標系」と言います。
そして運動方程式が成り立つ座標系を慣性系、
成り立たない座標系を非慣性系と呼ぶのです。
例えば車の中にいる時を思い出してください。
車が急ブレーキをかけると、
体が前のめりになってしまいます。
またブレーキをかけたりしなくても、
急カーブでは横に放り投げられそうになります。
でも、車の中の人は、
別に紐で引っ張られてるわけでも、
なにかに押されているわけでもありません。
つまり車の中では運動方程式が成り立っていません。
車の中は非慣性系だということです。
じゃあ運動方程式は万能じゃないじゃん…
とがっかりする必要はありません。
「慣性力」を定義することで非慣性系は慣性系に変換できます。
これについては以下で詳しく解説します。
【合わせてチェック】
・慣性力とは？東大院生が徹底解説！【高校物理】
まとめると以下のようになります。
・慣性系なら運動方程式が成り立つ
・非慣性系（座標系が加速度運動）
では運動方程式が成り立たない！
→しかし慣性系に変換可能
物理学的な問題②「力がわからない」
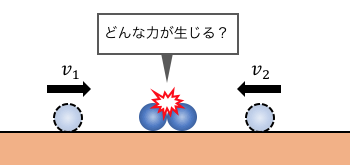
力がよくわからない場合や、
力が変化しまくってごちゃごちゃする場合、
運動方程式を使うのが難しいことがあります。
そういう場合には、
代わりに運動方程式と同値な式を使います。
運動方程式と同値な式とは、
・エネルギー保存則
・運動量保存則
です。
これらについては以下で詳しく解説しています。
【合わせてチェック】
・今すぐ使える力学的エネルギー保存則！
・運動量保存則を解説！運動量・力積の定義から丁寧に
運動方程式を直接用いないにしても、
結局、運動方程式の恩恵を受けていることに代わりはありません。
ここまでは物理学という学問として、
つまづきやすいところの説明でした。
ここからは、
学問的に本質的ではないけど、
高校物理の指導要領的に生じる問題を解説します。
高校物理の問題①「単振動」
ここでは「単振動」を知っている前提で解説します。
まず単振動の運動方程式の一例を書きましょう。
\[ m\frac{d^{2}x}{dt^{2}} = -kx \]
ここでは加速度を微分の形で書きました。
実はこの式は高校数学の範囲では解くことができません。
高校で習う微分は\(\frac{dy}{dx}=x\)や\(\frac{dy}{dx}=sinx\)など、
左辺にyの微分、右辺にxの形になります。
しかし単振動の運動方程式は、
左辺がxの微分、右辺にxの形になっています。
(xはtの関数であることに注意)
これは高校範囲では解けないため、
解いた結果を覚えて使うことしかできないのです。
ちなみにこれを解くと以下のようになります。
\[ x = Asin(\omega t + \theta_{0}) \]
単振動のより詳しい解説は、
以下の記事をごらんください。
【合わせてチェック】
・力学の最難関！単振動とは？東大院生が徹底解説！【高校物理】
高校物理の問題②「円運動」
ここでは「円運動」を知っている前提で解説します。
これまで見てきた運動方程式は、
xy座標で考えることを前提としてきました。
しかし、円運動は、
半径一定の円周上を動く運動であるため、
xとyで考えるよりも、半径と角度で考えたいのです。
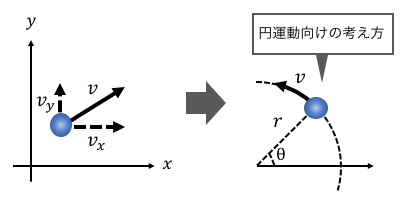
円運動を考えるときには、
「見方」を変える、つまり座標系を変えます。
これによって運動方程式の形も以下のように変わります。
\[ m\frac{v^{2}}{r}=F_{中心力} \]
見た目は違う式ですが、
これも結局は運動方程式です。
ただ座標系の説明は高校で習わないので、
「円運動特有の公式がある」と覚えている人も多いでしょう。
しかし実は円運動も運動方程式で考えることができます。
より詳しい解説は以下の記事をごらんください。
【合わせてチェック】
・【図解でわかる】円運動を東大院生が解説！速度・加速度の求め方
まとめ
今回は運動方程式の解説でした。
まだ習ったばかりの人はとりあえず使えるように、
力学を一通り勉強した人は、後半の内容を理解してみてください。
この記事の内容をきちんと理解すると、
問題を解く時の指針がかなり明確になると思います。
力学を一通り勉強したのに読み飛ばした人は、
ぜひ何度も復習してみてください。
