反発係数の意味をイメージしよう！エネルギー保存則との関係まで解説

あなたは反発係数の定義の「意味」がわかりますか？

また反発係数の使い方を理解できていますか？

反発係数は、
エネルギー保存則と結びつきが強く、
これらの関係を理解しておくことが重要です。

逆にこの関係を知らないと、
実際の入試問題で立式に困りかねません。

ここでは反発係数を詳しく解説していきます。

この記事を読むことで、
反発係数を網羅的に理解することができ、
力学の問題の見通しがよくなるでしょう。

後半には上級者向けに、
反発係数とエネルギー保存則の関係についても、
詳しく解説しています。

ぜひ最後まで読んでみてくださいね。

反発係数とは

ボールが壁にぶつかる場面を考えましょう。

前回勉強したエネルギー保存則を考えれば、
速さ10m/sでぶつかれば、速さ10m/sで帰ってきそうです。

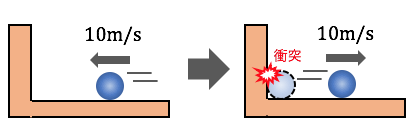
しかし、壁の材質によっては、
ぶつかった勢いを吸収されたりして、
跳ね返る頃にはスピードが落ちてることもあります。

ボールがぶつかる瞬間に、
大きな音が鳴ったり、壁が振動したりして、
運動エネルギーが別のエネルギーに変わり、
スピードが落ちているのです。

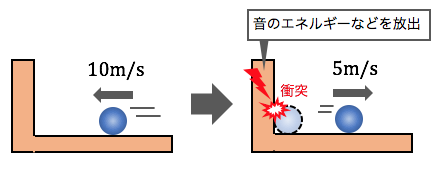
このように、壁の材質によって、
物体の「跳ね返りやすさ」が違います。

この跳ね返りやすさを「反発係数」というのです。

先ほどの例では、
速さ10m/sが衝突によって速さ5m/sに、
つまり速さが\(\frac{1}{2}=0.5\)倍になっています。

この場合、
壁とボールの反発係数は0.5である、
といいます。

このように反発係数は、
ぶつかる前と後の速さの比で定義され、
物体の跳ね返りやすさを表しているのです。

これが反発係数の考え方です。

それでは次の章で、
より一般的な反発係数の定義を見ていきましょう。

反発係数の定義

それでは「反発係数」を、
もう一度きちんと定義しましょう。

繰り返しになりますが、
これはぶつかる前と後の速さの比を表します。

さらに、上の定義では絶対値を外したときに、
分数の前にマイナスがついていますが、
これは衝突の前後で向きが変わることを意味します。

だからこの式を式変形すると、
逆向きに、\(e\)倍の大きさの速度になるよ
という式になります。

次に、少しだけ話を進めましょう。

以下のような2つのボールの衝突を考えます。

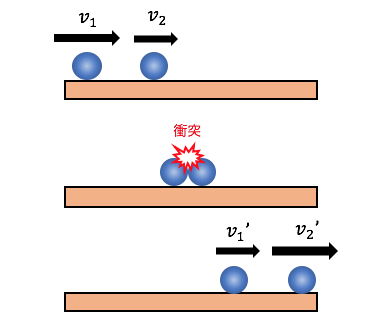
この場合は壁への衝突とは違い、
衝突する2つのボールの速度が両方変化します。

このような場合も、
反発係数の定義は変わりませんが、
片方のボールからの相対速度で考えます。

具体的には、衝突前の相対速度は、

\[ v_{前} = v_{1} – v_{2} \]

衝突後の相対速度は、

\[ v_{後} = v_{1}’ – v_{2}’ \]

となりますから、
反発係数は以下のようになります。

\[e = -\frac{v_{1}’ – v_{2}’}{v_{1} – v_{2}}\]

「相対速度」に慣れていないと、
少し難しい考え方かもしれませんね。

相対速度に不安がある場合は、
以下の記事で詳しく解説しているので、
ぜひそちらをごらんください。
【合わせてチェック】
（相対速度の記事は準備中です。）

ということで、結局、
反発係数の定義は以下のようになります。

反発係数の使い方

最後に反発係数の「使い所」を考えてみます。

反発係数は、物体が衝突するときに、
力学的エネルギーが保存しないことを
表したものでした。

よって反発係数は、
非弾性衝突でエネルギーが減ることを
数式に表すときに使います。

少し難しい考え方なので、
具体的な問題で確認してみましょう。

まずこれらの問題に共通することとして、
求めたい変数が2つありますから、
2つの式を連立して解く必要があります。

これを前提に、
まずは(1)から見ていきましょう。

(1)はエネルギーも運動量も保存しているので、
両保存則を使うことができます。

\begin{align*}
m_{1}v_{1} + m_{2}v_{2} &= m_{1}v_{1}’ + m_{2}v_{2}’ \\
\frac{1}{2}m_{1}v_{1}^2 + \frac{1}{2}m_{2}v_{2}^2 &= \frac{1}{2}m_{1}v_{1}’^{2} + \frac{1}{2}m_{2}v_{2}’^{2}
\end{align*}

あとはこれらを変形するだけです。
具体的な式変形は省略しますが、
計算結果は以下の通り。

\begin{align*}
v_{1}’ &= \frac{ (m_{1}-m_{2})v_{1} + 2m_{2}v_{2} }{ m_{1}+m_{2} }\\
v_{2}’ &= \frac{ 2m_{1}v_{1} + (m_{2}-m_{1})v_{2} }{ m_{1}+m_{2} }
\end{align*}

次に(2)です。

今回も外部からの力はなく運動量は保存しますが、
非弾性衝突なのでエネルギーは保存していません。

よってエネルギー保存則の代わりに、
反発係数の式を使って式を立てます。

\begin{align*}
m_{1}v_{1} + m_{2}v_{2} &= m_{1}v_{1}’ + m_{2}v_{2}’ \\
e = -\frac{v_{1}’-v_{2}’}{v_{1}-v_{2}}
\end{align*}

ただなんとなく式を立てているのではなく、
エネルギーが減少することを表していることに注意しましょう。

これを解けば以下のように求まります。

\begin{align*}
v_{1}’ &= \frac{ (m_{1}-em_{2})v_{1} + (1+e)m_{2}v_{2} }{ m_{1}+m_{2} }\\
v_{2}’ &= \frac{ (1+e)m_{1}v_{1} + (m_{2}-em_{1})v_{2} }{ m_{1}+m_{2} }
\end{align*}

エネルギー保存則と反発係数の定義、
これをきっちりと理解しておくと、
問題を解く時の見通しもよくなりますよ。

補足：エネルギー保存則との関係

何度も述べたように、反発係数1は
力学的エネルギーが保存することを指します。

つまり、
運動量保存則とエネルギー保存則で考えるのと、
運動量保存則と反発係数e=1で考えるのは同値です。

この章ではそれを示しておきます。

まずは運動量保存則とエネルギー保存則から、
考えをスタートします。

\begin{align*}
m_{1}v_{1} + m_{2}v_{2} &= m_{1}v_{1}’ + m_{2}v_{2}’ \\
\frac{1}{2}m_{1}v_{1}^2 + \frac{1}{2}m_{2}v_{2}^2 &= \frac{1}{2}m_{1}v_{1}’^{2} + \frac{1}{2}m_{2}v_{2}’^{2}
\end{align*}

少しテクニカルにはなりますが、
エネルギー保存則を以下のように変形していきます。

\begin{align*}
\frac{1}{2}m_{1}v_{1}^2 + \frac{1}{2}m_{2}v_{2}^2 &= \frac{1}{2}m_{1}v_{1}’^{2} + \frac{1}{2}m_{2}v_{2}’^{2} \\
m_{1}v_{1}^2 – m_{1}v_{1}’^2 &= – m_{2}v_{2}^2 + m_{2}v_{2}’^2 \\
(m_{1}v_{1} – m_{1}v_{1}’)(v_{1}&+v_{1}’)\\
=-(m_{2}v_{2} &- m_{2}v_{2}’)(v_{2}+v_{2}’)
\end{align*}

ここで運動量保存則が、

\[ m_{1}v_{1} – m_{1}v_{1}’ = m_{2}v_{2}’ – m_{2}v_{2} \]

であることを利用すると、
両辺の2つのカッコのうち、
前者を消すことができます。

\begin{align*}
(m_{1}v_{1} – m_{1}v_{1}’)(v_{1}&+v_{1}’)\\
=-(m_{2}v_{2} &- m_{2}v_{2}’)(v_{2}+v_{2}’) \\
v_{1}+v_{1}’ &= v_{2}+v_{2}’
\end{align*}

これをさらに変形していくと、
反発係数が1という式になります。

\begin{align*}
v_{1}+v_{1}’ &= v_{2}+v_{2}’ \\
v_{1}-v_{2} &= -v_{1}’+v_{2}’ \\
1 &= -\frac{v_{1}’-v_{2}’}{v_{1}-v_{2}}
\end{align*}

このようにして、
エネルギー保存則が成り立つことは、
反発係数が1であることに等しいとわかりました。

この計算ができる必要はありませんが、
一度見ておくと頭が整理されると思います。

まとめ

もう一度反発係数の定義を確認しておきましょう。

反発係数は入試問題でも頻出なので、
ぜひ手元の問題集で練習をしておいてください。