これは「エネルギー保存則」の説明の前に、
エネルギーの解説を行うための記事です。
もうエネルギーの学習が十分であれば、
いきなり保存則を確認してもいいでしょう。
【合わせてチェック】
・今すぐ使える力学的エネルギー保存則!
この記事はエネルギーの解説ですが、
そのためには「仕事」を理解する必要があります。
ということでまずは、
仕事の解説から順番に進めましょう。
目次
仕事とは
物理学において「仕事をする」とは、
物体に力を加えて移動させること
を指します。
そして一定の力\(F\)で距離\(x\)だけ動かした場合、
その仕事の量\(W\)は以下のようになります。
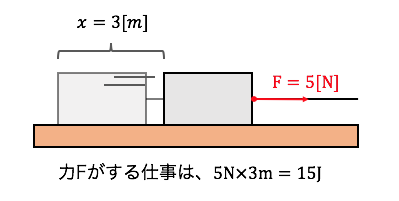
例えば以下のように、
床に置かれた箱を5Nの力で3mだけ、
引っ張ったとしましょう。
この時引っ張る力は、
\(W=5\times3=15[J]\)の仕事をしたことになります。
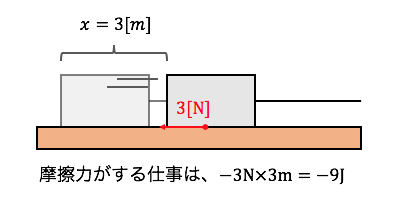
さらにこの時、
床がとってもザラザラしていて、
箱には摩擦力が3Nかかっていたとしましょう。
すると3m移動する間ずっと、
箱の動きを邪魔する方向へ3Nの力がかかります。
つまり摩擦力は、
\(W=(-3)\times3=-9[J]\)の仕事をしているのです。
このように仕事とは、
物体の運動をどれくらい助けたか、
物体の運動をどれくらい邪魔したか、
というような量になります。
次の章ではもう少し詳しく仕事の定義を見ていきます。
より正確な仕事の定義
さていくつか具体例を見たところで、
もう一度仕事の定義をしっかりと考えてみます。
このサイトで勉強してきて、
運動量と力積の記事を読んだ人なら、
この先の流れが想像できるかもしれません。
先ほどの仕事の定義では、
力がずっと一定である場合を考えてきましたが、
実際は力が一定とは限りません。
力が物体を動かす間に、
例えば以下のように力が変化するかもしれません。
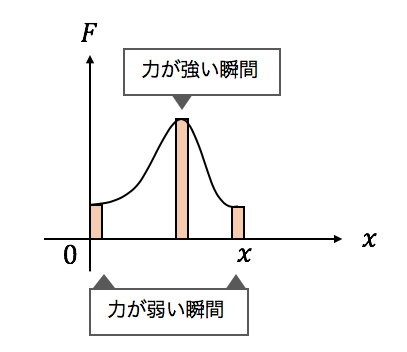
弱い力からぎゅーっと力を強め、
最後は徐々に力を抜いていった感じです。
最初はゆっくりと仕事をして、
一番力を込めた瞬間に最大限の仕事をして、
最後はまたゆっくりと仕事をしています。
つまり加速度や力積同様に、
仕事も図の面積の部分になります。
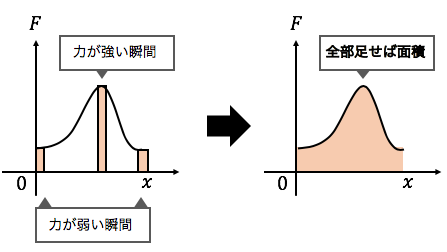
よってより正確な仕事の定義は以下の通り。
仕事の注意点
仕事は物体の移動をどれだけ助けたか、
物体の移動をどれだけ邪魔したか、
でしたね。
だから、
物体の移動と同じ方向の力しか
仕事をしているとはみなしません。
例えば先ほどの例で、
常に垂直抗力や重力も働いていますが、
これらは移動に関係ないので仕事をしていません。
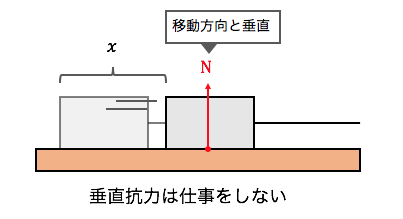
また紐を引っ張る時に、
真横ではなく、斜めに引っ張ったとしましょう。
このとき加えた力のうち、
移動方向に水平の成分は仕事をしますが、
移動方向に鉛直の成分は仕事をしません。
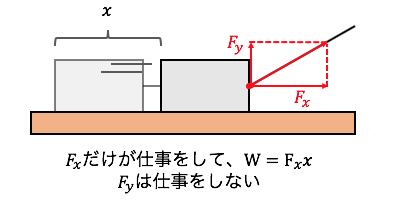
先ほどは断りなく力\(F\)と書きましたが、
正確には運動の向きに沿った力だったということです。
エネルギーとは
仕事を定義することで、
ようやく目的だった「エネルギー」を考えられます。
エネルギーという言葉を聞くと、
ガソリンや電池、体力ややる気
などが頭に思い浮かぶかもしれませんが、
これらは全て物を動かす原動力です。
つまりエネルギーとは、
物体が持っている仕事をする能力
のことです。
高校の力学では主に、
①運動エネルギー
②重力による位置エネルギー
③弾性力による位置エネルギー
が登場します。
次の章から、これらの意味や、
どんな数値をとるのかを考えていきましょう。
①運動エネルギー
速度を持っている物体がぶつかると、
ぶつかった物体を動かせますよね。
つまり速度を持った物体は仕事をする能力があり、
その能力を「運動エネルギー」と呼びます。
では運動エネルギーの大きさを考えていきましょう。
まずは物体\(m\)が速度\(v\)で運動しているとします。
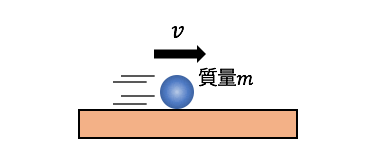
この物体に力Fをかけることで、
無理やり速度を0にしたとしましょう。
これは力Fが物体に仕事をして、
運動エネルギーを打ち消したことになります。
つまり力Fがした仕事Wこそが、
物体の運動エネルギーだということです。
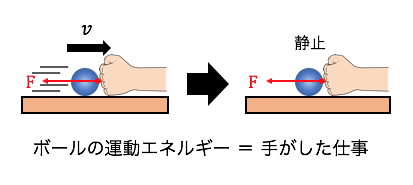
では実際に計算してみます。
今回使う公式や法則は、
・\(W=Fx\) (力一定より)
・\(ma=F\)
・\(v_{後}^{2}-v_{前}^{2}=2ax\)
です。
まずは運動方程式を考えますが、
力Fは運動の逆向きにかかっていることに注意すると、
\[ ma = -F \]
次に3つ目の公式から、
\[ 0^{2}-v^{2}=2ax → ax = -\frac{1}{2}v^{2}\]
以上を使えば、
\begin{align*}
W &= Fx \\
&= -max \\
&= -m × (-\frac{1}{2}v^{2}) \\
&= \frac{1}{2}mv^{2}
\end{align*}
このようにして運動エネルギーが求まりました。
W&=\int Fdx=m\int\frac{dv}{dt}dx\\
&=m\int\frac{dx}{dt}dv=m\int vdv\\
&=\frac{1}{2}mv^{2}\end{align*}
②重力による位置エネルギー
高いところに物体を持ち上げて落とすと、
ドスンッと地面に衝撃を与えます。
このように物体は、
高いところに持ち上げるだけで、
仕事をする能力を得ることができます。
これを「重力による位置エネルギー」と呼びます。
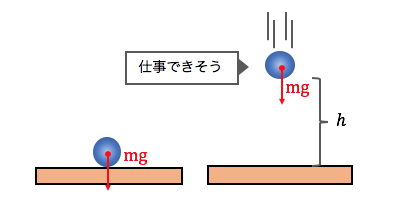
ではこちらも値を計算してみます。
地面にある物体には\(mg\)の重力がかかっています。
これに逆らうように\(F=mg\)の力を加え、
高さ\(h\)まで持ち上げるとしましょう。
この時に与える仕事Wが、
重力による位置エネルギーになります。
\[W=mg×h=mgh\]
③弾性力による位置エネルギー
ばねに物体をくっつけて、
ぎゅっと押し付けたり引っ張ったりすると、
物体が動き出しますね。
このようにばねは物体に仕事をする能力があり
それを「弾性力による位置エネルギー」といいます。
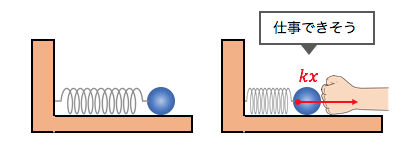
これまで同様に値を計算してみます。
重力の時と同じように考えれば、
ばねの自然長の状態から位置xまで押すとき、
必要になる仕事Wが弾性力による位置エネルギーです。
しかし重力と違って少し注意が必要です。
ばねは押せば押すほど力が増しますから、
力Fが一定にはなりません。
グラフで書けば以下の通り。
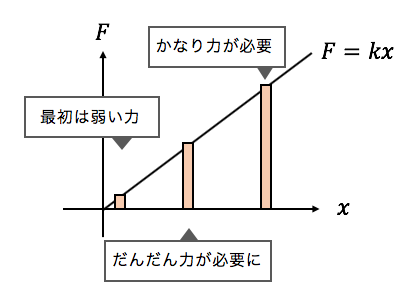
最初の方はほぼ力0で動き、
徐々に力が増えていって最後はkxになる、
その間に必要な仕事はグラフの面積です。
グラフが三角形であることに注意すれば、
\[W = \frac{1}{2}\cdot x \cdot kx = \frac{1}{2}kx^{2}\]
\[ W = \int kxdx = \frac{1}{2}kx^{2} \]
エネルギーまとめ&参考
運動エネルギー \[ K=\frac{1}{2}mv^{2} \]
重力による位置エネルギー \[ U=mgh \]
弾性力による位置エネルギー \[ U=\frac{1}{2}kx^{2} \]
力学の分野で出てくるエネルギーは以上です。
参考ですが、
万有引力による位置エネルギー
静電気力による位置エネルギー(=電位)
なども今回と同じような考え方で得られます。
なんとなーく覚えるのではなく、
仕事との関係を意識できるといいですね。
まとめ
今回は仕事・エネルギーの解説でした。
仕事は「力が物体をどれだけ移動させたか」
というわかりやすい量です。
一方エネルギーはフワフワしがちですが、
物体が仕事をする能力と、仕事を基準にするとかっちり理解できていいですね。
次回はエネルギー保存則を見ていくので、
楽しみにしていてください。














コメントを書く